随着人们对于通讯网路以及档案传输的需求与日俱增,高效能通讯系统俨然已成为现今最为重要的发展议题。但因通讯传输速率大幅提升,时脉抖动(jitter)对于系统将会造成严重的影响,所以不管任何相关产品皆必需通过抖动量验证后才可进入量产。有鉴于此,在本文中将提出一内建抖动测试架构,也就是采用抖动放大原理搭配脉波吞噬(Pulse Remove;PR)之技术,实现出更准确及更有效率的内建抖动测试电路,以减少外部仪器之需求进而大幅降低生产测试成本。
前言
时序抖动(timing jitter)为系统设计中普遍存在的问题。但是因为早期系统使用需求量不高,所以皆透过较低的讯号传输速度减少设计负担,也因此抖动相较于整个周期时间所占的比例非常微小。随着积体电路日新月异,人们普及使用电脑并增加通讯频宽需求,在各种通讯协定上都大幅增加其操作速度。在相同条件下时序抖动已在讯号间占有相当大的百分比。因此与时脉相关的系统都会针对抖动做进一步的规范。
目前抖动量萃取的方式皆藉由仪器外部量测所得,但当系统操作速率增加后于量测上会遇到以下两个问题:测试成本(cost)与测试准确度(accuracy)。从测试成本观点来看,若要量测GHz以上讯号,示波器为得到准确量测数值其取样率必须非常高速,动辄数十GS/s。因此软硬体实现变得非常困难,测试机台成本也就大幅提升。此外,采用外部仪器测试晶片内部讯号,也会产生量测可靠度的问题。例如测试环境对于待测讯号的干扰、I/O介面频宽之限制、晶片内部输出缓冲器(output buffer)的杂讯…等等,这些皆会造成量测数值准确度下降。
为解决相关测试问题,目前备受瞩目的方法就是加入可测试性设计(Design for Testability;DfT)。可测试性设计的观念是在设计流程中加入量测的考量,或是藉由一些额外辅助运算方式来降低对自动测试设备性能的要求、及大幅降低生产测试所需之成本与时间。然而此测试方式虽可减少测试成本和时间,但最被市场所诟病的是其准确性。这是因为额外电路将会注入杂讯于待测电路中,且也无法确保此电路设计是否完善;此外利用额外的运算方式必须先确保待测数值或是待测环境设定无误,否则就算大幅缩短测试时间也是徒劳无功。
本文将提出一可内建于晶片中量测时脉抖动量之测试想法与架构。其采用单撷取(single-shot)量测方式搭配时间放大的技巧将讯号抖动量等倍率增加,来减轻时间数位转换电路(Time-to-Digital Converter;TDC)在制程上的限制、进而提升测试解析度(resolution)。此外搭配使用脉波吞噬之电路技术,使得架构具有极佳线性度。相较与传统内建抖动量测电路([1]~[5]),其具备宽频操作以及低抖动量测试之特性,并有较小的超额面积率(area overhead)。
Background
发展至今,内建时脉抖动测试技术有几种较为普遍的测试架构,有些已应用于业界产品测试中,先针对这些传统架构做进一步介绍。
Delay Chain [1]
《图一 使用delay chain之抖动量测法》
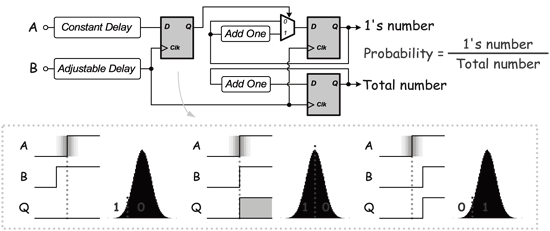
此测试架构为Logic Vision于1999年提出,是利用可调整延迟线(Adjustable Delay Line;ADL)、正反器与计数器搭配统计原理来测试抖动量。正反器就好比是一个相位检测器,若调整延迟量使得B领前A,此时0出现的机率将占多数;反之当B落后于A,则1出现的机率将占多数。亦即藉由调整不同延迟量来得到不同机率分布,再搭配上累积分布函数的运算(Cumulative Distribution Function;CDF)将抖动量运算出来。
优点:
●架构简单且容易实现。
缺点:
●延迟线会有频率的限制,此将影响操作范围。
●需调整延迟时间来得到1、0分布进而得知抖动量,因此将需冗长的测试时间。
Two Ring Oscillators [2]
《图二 使用two ring oscillators之抖动量测法》
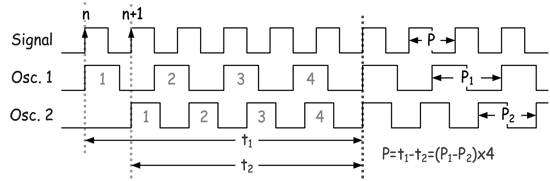
此测试架构则为Credence于1999年所提出,是使用两组已知但不同操作频率的内建振荡器,利用待测时脉讯号的第n个与第n+1个周期分别去触发振荡器使其开始振荡。当两者不同周期时脉之相位吻合后,再利用相位吻合所需的周期数搭配振荡周期即可反推时脉抖动量。
优点:
●采用触发振荡的方式,讯号不会因为经过delay chain后duty cycle而受到影响,相较于前面的作法具有较广的量测范围。
缺点:
●抖动量是经多个周期比较后所得,因此测试时间将是最大的考量。
●使用两组振荡器之相位比较来得到抖动量,若振荡频率漂移将造成测试误差。
●需额外的统计电路辅助,成本较高。
Vernier Delay Line [3]
《图三 使用vernier delay line之抖动量测法》
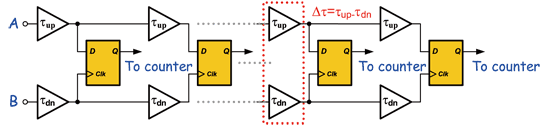
游标延迟线(Vernier Delay Line;VDL)为目前最常被采用的抖动测试技术,由Piotr Dudek于2000 JSSC所发表。操作原理是将参考与待测时脉分别送入两个不同延迟量(τup与τdn)的delay chain中,若两者间有抖动量存在,经延迟单元后其会相互逼近。当在n个周期后两讯号同相位或是相位领前、落后的状态改变,即可算出抖动量为nx△τ,当中△τ=τup-τdn。所以藉由此测试技术将可测试低于次逻辑闸(sub-gate)的抖动量。
优点:
●使用延迟时间差的观念来实现,可具有较佳的测试解析度(=△τ)。
缺点:
●制程变异下无法确保每个延迟单元之延迟时间量相等,此将影响测试准确度。
ADC Sampling [4]
《图四 使用ADC sampling之抖动量测法》
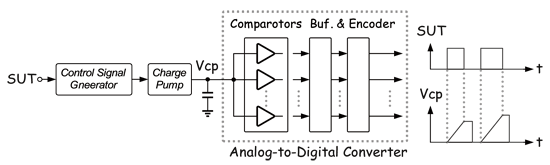
因抖动为时间的变化,所以一般测试架构都是从时间观念来得知。但Henery C. Lin于2003 ITC中,利用时间转电压的方式来实现抖动量测试。简单来看这就是一组电荷帮浦,当待测讯号为高电位时电流会对负载充电;而在低电位时就将电压位准重置归零。所以待测讯号脉波宽度越大,所得的电压值也就越高;反之脉波宽度较小电压也就随之降低。接着再利用ADC将电压位准转换成数位码以求得抖动量。
优点:
●于低速时脉测试中具有较高之解析度。
●采用real time的输出,测试时间将可缩短。
缺点:
●测试解析度与测试速度皆取决于ADC之设计。
●于低压操作时易受垂直抖动影响进而导致解析度大幅下降。
Component-Invariant VDL [5]
《图五 使用component-invariant VDL之抖动量测法》
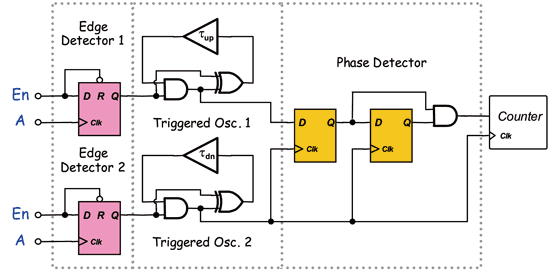
最后一种测试架构为G. W. Roberts于2001 ITC所提出。此种采用非变异量元件之游标延迟线和[03]的做法其实非常相似。其是利用一级的延迟单元然后让讯号回授振荡,如此一来将可确保量测解析度皆为△t。若于n个振荡周期后两个延迟量相位改变或是相同时,则可依[03]的作法计算出抖动量。
优点:
●每级延迟皆为△t,提升量测准确度。
●使用两个延迟量之差来量测抖动量,因此可具有较高解析度。
缺点:
●和[02]架构一样需较长的测试时间。
由以上所提出的五种测试法可看出,以目前的测试技术而言,不外乎是利用signal amplitude sampling以及time domain analysis两种方法来实现。但以前者来说,随着制程进步操作电压降低,此作法将面临ADC设计的瓶颈,所以近年来已较少人采用此作法来实现抖动量测试。后者虽各架构实践方式有所不同,多数是利用时间数位转换(Time-to-Digital Converted)的观念来实现。然而这些架构都有共通的问题,就是操作速率不快以及解析度不高。以目前市面上PC周边产品来说,普遍速度皆属于几百MHz等级,而CPU或是传输介面则会上看至GHz等级。另外抖动量在高速系统中最大值约定义在数十ps,所以若测试系统没有好的解析度和宽范围测试之能力,将无法判别待测讯号之好坏。因此本文将提出一个新的抖动测试想法与架构,针对高速与低抖动时脉作更精确(precision)与更准确(accuracy)之抖动测试。
Proposed Technique
《图六 传统时间-数位转换过程之示意图》
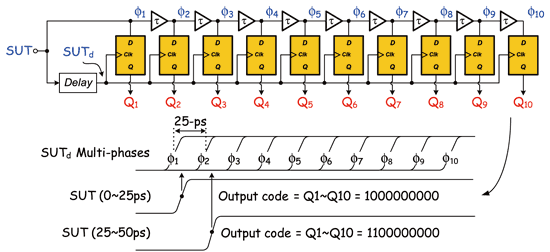
在介绍我们所提出之测试方法前,先来探讨传统测试的问题。图六为传统时间-数位转换的过程。当一时脉(SUT)发生抖动时,其边缘会离开原本理想的位置,此时普遍的做法会将SUT延迟一个周期时间(SUTd)后去测量En和En+1边缘之抖动程度。而测试方法就是将SUT送入delay chain中当作被取样的资料,而SUTd则作为取样时脉。当SUTd对经过不同延迟量之SUT做取样后即会产生出温度码(thermal code)的数位资料,此输出资料即代表不同时脉抖动量。
举例来说,若目前delay chain为10级25-ps延迟量之延迟单元所组成,此时时脉周期对周期抖动量为10-ps,经取样后会得到1000000000的数位码;而若当抖动量为30-ps,则会产生1100000000。因此抖动量越大,数位码中的1也就会越多。所以目前的技术皆是以此种想法来实现抖动量测试,而不同之处就是会利用许多电路技巧将延迟单元的延迟量缩小以提高测试解析度,如游标延迟线、内插…等。
但从上述说明即可得知,因为解析度和延迟单元之延迟量成反比,所以若不将延迟量设计得非常小,相对地就会产生测试误差量。以前例来说,理想上当抖动量为0.1-ps和24.9-ps时所得到的数位码皆为1000000000,其最大误差量接近一个延迟时间。所以说若在高速低抖动的应用中,此测试误差量将无法说服测试使用者。但假若利用电路上的技术缩短延迟时间减少误差量,其还是会因制程限制有极限值存在,且通常会耗费较大的硬体面积。所以我们反向思考,不以时间-数位转换器为出发点,而是以一简单电路技术先放大周期对周期之抖动量,如此一来即可减少测试电路设计的困难度并提升测试解析度。
《图七 抖动量放大之概念图》
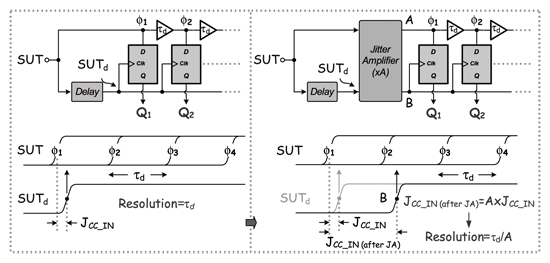
以图七为例,若延迟单元的延迟时间为τd,则代表在无任何辅助电路下其最佳解析度即为τd。但以所提出的观点来看,若此时先将输入抖动量放大A倍送入delay chain中,效果就如同将延迟时间缩短来增加测试解析度,也代表此时整个架构最佳解析度便可等效成”τd/A”。
举例来说,于0.13-um制程中最小闸延迟时间为25-ps,所以采用传统作法大约只能量测到的抖动量为25-ps;但是若在抖动量转换成数位码前先将其放大25倍,则最佳解析度即提升至1-ps(25-ps/25)。除此之外,随着抖动放大倍率A大于τd后,因延迟单元的延迟时间小于1-ps(τd/A<1),所以此时将可针对sub-pico-second等级之抖动量作测试。
因此本抖动测试概念就是藉由放大输入时脉周期对周期之抖动量,进而补足时间-数位转换电路的不足,且更进一步提升测试解析度,以让此测试系统操作于高速低抖动量的系统具有极佳准确度。图八即为运用所提出之抖动放大原理所实现的内建时脉抖动量之测试架构。
《图八 所提出之内建时脉抖动量测试架构》
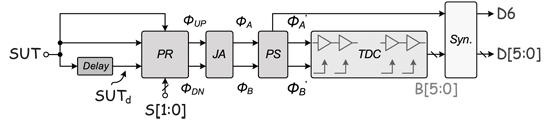
其包含了脉波吞噬电路(Pulse Remover;PR)、抖动放大电路(Jitter Amplifier;JA)、相位选择电路(Phase Selector;PS)、时间-输位转换电路(Time-to-Digital Converter;TDC)与同步电路(synchronizer)。其中PR和JA之组合是用来将输入抖动量做线性放大;而TDC的功用则可把抖动量化成数位码;另外同步电路会将所有的输出数位码作同步以利后续软体或硬体之分析。但在此输出只看的出周期对周期间之抖动量,并无法判断目前边缘间的关系(即相位)。
因此于TDC前插入一PS[6],其用于判断目前相位关系并决定ΦA与ΦB进入TDC前谁当作资料而谁当作取样时脉。若ΦA领前ΦB,则D6为Hi、ΦA’=ΦA、Φ’=ΦB、属于正向抖动;反之若ΦB领前ΦA,则D6为Low、ΦA’=ΦB、ΦB’=ΦA、属于反向抖动。利用此位元之结果将可更明确判断抖动之型态。接下来我们就针对各主要电路做进一部的介绍。
抖动放大电路设计架构 [7] [8]
《图九 抖动放大电路之架构图与时序图》

周期对周期抖动量即为后一个周期边缘En+1和前一个周期边缘En之相位误差,因此若要实现抖动量放大就必需将En和En+1间之边缘时间差拉大。在本文中将采用电流对负载充放电之原理来达到抖动放大之功能。我们以图九来说明其操作原理。
抖动放大电路基本上是由两组不同电流量之电荷帮浦(Charge Pump;CP)与决策电路(Decision Circuit;DC)所组成,而分别由待测讯号SUT、一个周期延迟后之讯号SUTd与两者之组合来控制。其最基本的想法为利用不同充电斜率(即充电速度)搭配讯号不同起始点(即转态边缘)之特性,来合成出具有较大抖动量的时脉边缘。而为了清楚解释其放大原理,我们将SUT(S)与SUTd((Sd)依相位关系区分成四个区间,然后分别探讨在不同区间内的操作情形。如表一所示。
(表一) 电荷帮浦操作状态表


搭配图九与表一之叙述,从中可以得知在初始状态时因SUT与SUTd为低电位,开关皆turn off,所以并无任何电流对负载做充电因此输出结果(f1、f2)将为低电位(VL)。但若当两个phase间有抖动存在时,SUT会为高电位而SUTd为低电位。此时f1会以(n+1)倍的电流对负载充电pull up,而f2因S3 turn off所以将保持前一状态的低电位。接着经过Δτ的时间后,SUTd也pull high,促使S3 turn on、S1 turn off,此时f1和f2将一起以I的速度往高电位移动。但是仔细观察Region II和Region III之过程,因在Δτ的这段时间里f1先以较快的速度启动,若Region III在相同充电的斜率条件下(电流量皆为I)其会先到达稳态位准;而接着再经过n*Δτ时间后,f2才也会到达此位准。此时从图九中可以看出f1、f2与所设定的临界电压(Vth)有两个交点,若用两组决策电路将转态点判断出来即可产生两组不同相位差的输出讯号(Out1、Out2)。所以利用上述之条件,我们可以简单以公式一来表示出输出与输入间的关系:
《公式一》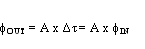
其中fOUT为Out1、Out2间的相位差(放大后之周期对周期抖动量)、fIN为SUT、SUTd间的相位差(放大前之周期对周期抖动量),而A即代表放大倍率。
利用上述概念,本创作即可将时脉讯号之周期对周期抖动量加以放大,来弥补时间-数位转换电路的不足。然而单纯光靠电流充电能力的行为模式来达成放大目的,会面临电路操作瓶颈进而导致测试误差产生,例如放大倍率的非线性或是操作频率变化等,接下来我们会针对这些效应提出解决之道。
抖动放大电路及Pulse Remover设计的分析
(表二) 符号表示

在抖动放大电路基本设计中,因为是使用电流对负载充放电之速率来达到抖动放大,因此先针对充放电位准以及时间作定义。如表二所示。
图十(a)中,通常抖动放大电路在低速率操作时,因其抖动量相较于半个周期时间所占的比例较小,因此电荷帮浦输出(f1、f2)到达高稳态点时间(ts1、ts2)通常会小于负缘转态点时间tf。
《图十 抖动放大电路时序图:(a)Case 1 : tf>ts2;(b)Case 2 : tf≈ts2;(c)Case 3 : tf
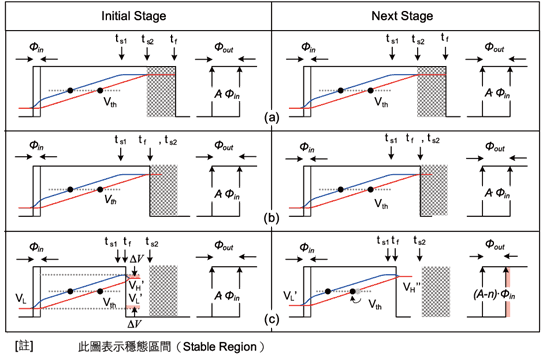
所以在此频段操作因有足够的稳态区间(stable region),其经决策电路后产生之输出相位差fOUT相较于输入相位差fIN几乎能维持定值,也就代表放大倍率A为constant。但若当待测时脉频率上升后,如图十(b)所示,随着讯号周期缩短tf之发生点提前,在tf非常接近但大于ts2时,抖动放大电路依然可勉强维持住放大倍率,所以此时即称为操作临界值。但假若不幸在所使用的应用中tf发生较大的变异或是操作频率继续往上升,导致ts2比tf晚发生,则放大倍率将开始产生非线性的变化。
从图十(c)可观察出在正常的操作模式下f1与f2最后皆会回到稳态位准VH、VL。但假若转态边缘tf在尚未稳定前就出现,则f1与f2之电压会被强制维持在新的位准上,也就是VH’(=VH-ΔV)与VL’(= VL +ΔV)。这个现象虽对于第一个周期(initial stage)之放大倍率没有造成影响,但是从图中得知,在下一个周期(next stage)中因为f1、f2电压起始位准点有了变化,所以经充电后与临界电压Vth的交点必然随之改变。换句话说就是voltage domain variation将转换成time domain之phase error,此时即会造成放大倍率变动。因此周期对周期抖动放大电路需操作在wide range之应用时,就必需利用一些机制控制稳态时间点ts比负缘转态点 tf早发生,如此才不会造成放大倍率的失真。有鉴于此,本文将提出一个使用脉波吞噬观念之单撷取量测方式来改善之。
脉波吞噬之单撷取量测方式
《图十一 脉波吞噬概念图》
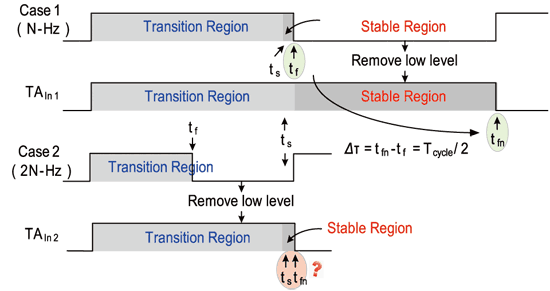
以上述讨论可知,若要实现tsf,不外乎是将稳态时间点往前拉会或者是延迟负缘转态点产生之时间。以电路实现角度而言,因ts是电流对负载充电后所产生的电压与高电位VH之交集,所以电流越大、回到稳态点能力越强,相对其出现时间会越早。但抖动放大的产生就是藉由不同速率电流之差所得,想必然放大倍率也将受到影响。所以为了兼顾放大倍率与电流量间trade-off,本文将采用延迟tf之作法来维持不同操作频率下的抖动放大倍率。
如图十一case1所示为一低频操作时的示意图。为了让抖动放大电路的放大倍率维持定值,待测讯号的ts必需小于tf,而worst case会发生在ts等于tf的时间点,此时稳态区间几乎会近似于零,也就是说放大倍率会非常不稳定。
为了改善这个问题,以先前的说法就必需将tf时间点做延迟。简单来看就是把测试速度放慢,利用脉波吞噬电路移除掉0.5个周期,来换取稳态区间之宽度。如图所示,若把case1的讯号做处理后成为TAIn1,其负缘转态时间点发生的时间往后延迟了Δτ(=tfn-tf=Tcycle/2),这代表着稳态区间随之放大2倍。因此若把待测讯号的频率增加后,其因具有足够的稳态时间,所以放大倍率将不受到clock variation和频率变动之影响。
但在图十一 Case2中,待测时脉讯号操作速度持续上升(约为Case1的两倍),可以很明显观察到若不采用脉波吞噬机制,ts已远远超越了tf,此时抖动放大电路之放大倍率已为非线性操作;但若加入脉波吞噬的机制后,因待测讯号速度太快,在相同充放电的速率条件下,ts也非常靠近tfn,放大倍率变异的问题还是存在。所以由此可知真正要达到wide range的操作,不管在任何频率下,皆需要拥有相同的稳态区间,才会真正得到constant之放大倍率。有鉴于此,我们将脉波吞噬的机制稍做修改,将不再维持固定移除0.5个周期,而是随着待测物的频率每增加一倍而随之变化,其remove number可由公式二表示之:
《公式二》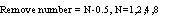
其中N为频率变化率。在本文中所提出的例子因为要达到数十MHz~1.6GHz之操作,所以将100MHz定为基准,频率每增加一倍就必需改变remove number来维持放大倍率。如图十二所示。
《图十二 于各操作频段间之脉波吞噬概念图》
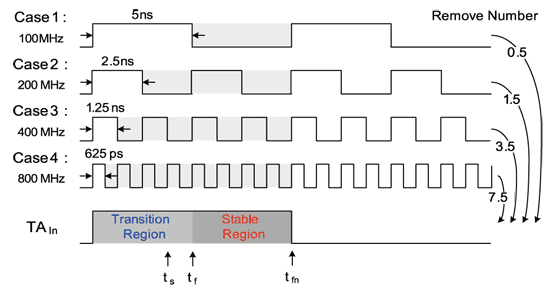
以电路的角度而言,要实现图十二脉波吞噬电路其实不难,只要将待测讯号依频段经过相对应的除频器即可实现。但实际上若直接把待测讯号经过除频器来达到脉波吞噬,依参考文献[9]之说法,该讯号的抖动也同时间会被放大,约为 √n倍。此外,除16的电路最少需要4组DFF来实现,代表待测讯号到达抖动放大电路前就必需经过许多transistor,进而受到power noise或是thermal noise干扰导致抖动上升,这将会严重影响量测准确度。
以边缘检测达到脉波吞噬效果
《图十三 (a)所提出之抖动放大电路;(b)边缘检测电路操作示意图》

因此本文将采用边缘检测(edge detection)之技术来达到脉波吞噬的效果,如图十三(a)所示。其主要包含两大方块:边缘检测器与脉波吞噬电路。首先,当待测讯号启动后,为了维持放大倍率,需先进行pulse remove的动作。以图十三(b)为例,SUT为待测讯号,EN为脉波吞噬电路所产生,E为经过处理后的待测讯号。其中脉波吞噬电路是由MUX所实现,其可藉由控制s脚位来选择EN讯号为SUT之/2、/4、/8、/16的结果。
此外EN接至边缘检测器的data input端,而SUT则接至clock input端。当EN为高电位时,SUT 正缘产生后会取样到Hi,因此讯号E马上pull Hi。若此时我们选择remove为/8时,如图十二Case3所示,EN讯号会维持4*TSUT的时间后转为低电位,因此当SUT下一个正缘产生后,其会取样到Low,促使讯号E pull down。
由图中可以看出,讯号SUT经转换后成功remove掉3.5(=4-0.5)个cycles,且SUT讯号只经过一颗ED。如此一来将可拉长stable region,维持放大倍率,并也不会因为让待测讯号路径太长而改变原先之抖动量。因此利用上述所提出抖动放大技术搭配脉波吞噬观念之单撷取量测法,将可在任何频段下线性放大待测时脉抖动,以利后段时间-数位转换电路之抖动量解析,并解决其因制程限制所造成准确度不足的问题。
时间-数位转换电路(Time-to-Digital Converter;TDC)
《图十四 所提出之时间-数位转换电路》
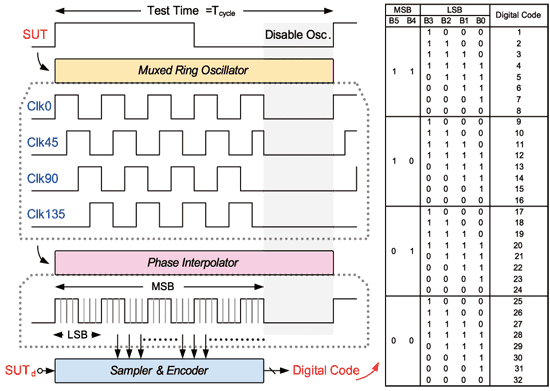
在本文中我们提出新的时间-数位转换电路,这是因为传统时间-数位转换电路基本上皆是使用多级缓冲器或是延迟单元来产生多相位讯号,然后藉由取样来得到数位码。然而以目前0.13-um的制程来说,其所能产生的最小缓冲延迟约为25-ps左右;亦即以整个系统来看,其能测试的最高解析度也等于25-ps,此规格在现今高速应用中已无法满足测试需求。
有鉴于此,我们将利用多工式振荡器搭配相位内插法,来实现一较高解析度之时间-数位转换电路。如图十四所示。其主要包含了一组多工式振荡器(Muxed oscillator)、相位内插电路(Phase Interpolator;PI)以及取样编码电路,当中多工式振荡器是用来产生多相位之参考讯号。相较传统使用open loop delay chain,close loop因有回授机制,所以会具有较准确的单位延迟时间,且较不易受到制程漂移之影响。另外因为是使用振荡原理来产生相位,所以可藉由测试振荡频推算出单位延迟时间,接着若再搭配使用内插电路技术,将可大幅提升测试解析度。
《图十五 多工式振荡器之电路架构图》
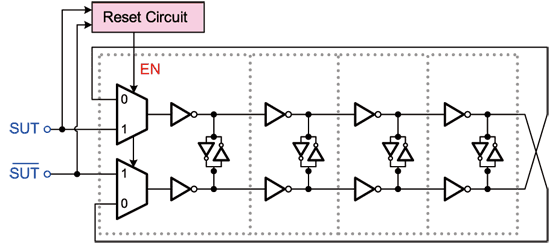
多工式振荡器是时间-数位转换电路中最为重要的电路,因为其必需依待测讯号的上升缘,来振荡出用来被取样之多相位高速讯号。如图十五所示,由两个多工器、四级延迟单元以及重置电路所组成。其称为多工式振荡器是因为此电路具有两种操作模式,分别为振荡模式(oscillating mode)与闩锁模式(latching mode),模式之切换则由重置电路来决定。
相关操作原理如下。当待测讯号正缘产生时,重置电路会输出EN为低电路,此时多工器选择到0。以图十五所示,此时回路可视为一差动振荡器,持续稳定提供多相位之高速参考讯号。然而通常于各系统中抖动量皆不会超越半个周期,也就是(1/2)xUI,所以其实每个周期内的抖动测试皆会于半个周期内结束,因此只需于待测电路的半个周期里产生出待取样讯号。换句话说就是只需让多工式振荡器工作半个周期后即可关闭。
因此当待测讯号负边缘一产生,重置电路会强制EN为高电位,此时多工器将由1的路径输出,也就是切换至闩锁模式。由图中可看出,此时整体振荡回路已被切断,输入即为待测讯号,各延迟单元的输出不是待测讯号的延迟、就是待测讯号的反向延迟,直至正边缘又产生后,才会恢复振荡模式以利抖动之测试。
传统时间-数位转换电路设计上,通常会受到制程所能产生的最小闸延迟所限定。为了克服此问题,我们采用了常见的相位内插电路,来产生小于一个延迟单元可提供的延迟时间。相位内插电路的直觉想法是希望能够在两个相邻相位的信号之间产生一个新的信号,而其相位会介于这两相邻相位信号间,进而达到提供更高相位解析度的信号 [10]。
小结
以上我们介绍内建抖动测试想法与架构,主要是想藉由放大输入抖动量来解决传统测试法无法测试低抖动量的问题,并搭配上多工式振荡之时间-数位转换电路,来提升整体系统解析度。此外也依电路操作特性提出一脉波吞噬电路,使得此测试系统将可于各频段进行自我测试,将不会因操作速度而影响测试品质。接着下一章节中,我们将利用HSpice来验证所提出之方法与架构。
模拟结果
《图十六 动放大电路之转移曲线图》
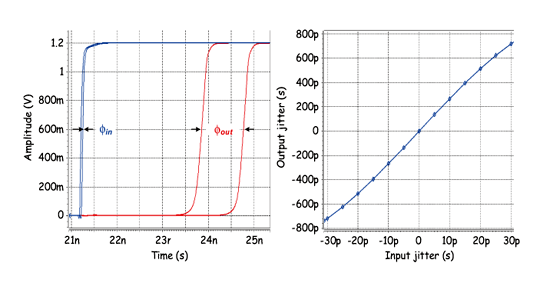
(X轴:输入抖动量;Y轴:输出抖动量)
内建抖动测试架构中最重要的元件为抖动放大电路,因为其放大倍率将影响系统解析度以及稳定度,所以首要工作就是确保抖动放大电路操作特性。如图十六即为抖动放大电路之模拟结果。当时脉抖动产生时,经由此电路可把时脉边缘扯开,也就是增加相位误差量。另外我们可利用不同输入抖动量来观测抖动放大电路之操作线性度,如图十七所示。若所模拟出来的转移曲线呈现相同斜率,代表此电路的放大倍率为一定值;但若曲线呈现出许多斜率,则可明显观察出放大倍率于不同输入抖动时具有不同的放大倍率,所以我们便需针对制程漂移对电路影响作模拟分析。
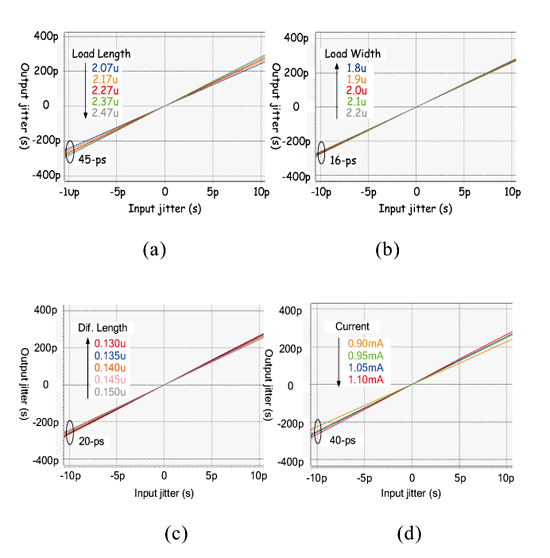
《图十七 放大倍率vs.制程漂移:(a)Load length;(b)Load width;(c)Diff. pair length;(d)Bias current》
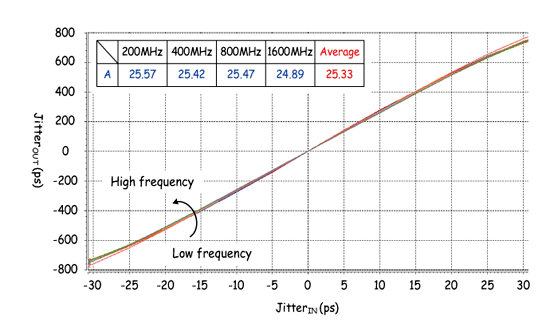
《图十八 放大倍率 vs. 操作频率》
抖动放大电路分析结果
先前介绍过抖动放大电路是藉由电流充放电速度来达到抖动放大,因此负载以及电容量将决定抖动放大的程度,所以以下就针对四个关键点作分析,并模拟其转移曲线图。由图十七所示,(a)~(d)分别为负载电晶体之length、负载电晶体之width、差动对电晶体之length和偏压电流变异时之模拟。从中可以观察出放大倍几乎皆维持在固定的倍率,但在负载电容(length)与操作电流变化时对于系统有较大的偏移量,约40-ps。
不过以整体系统来看,因为采用的是放大抖动量来测试,再将结果除以倍率得到原始抖动量,所以虽然模拟看出放大后的抖动约有40-ps的变异,但除以放大倍率25以后其变异约为1.6-ps,此误差量对于整体测试值几乎可忽略不计。此外,图十八为抖动放大电路操作于不同频段的转移曲线图。从中可明显发现,不论是在低频或是高频操作时,其皆具有近似的transfer curve,所以即验证此抖动放大电路具有宽操作范围以及线性抖动量放大之特性。因此由以上模拟可知,我们所提出之抖动放大架构将可运用在抖动测试系统中。
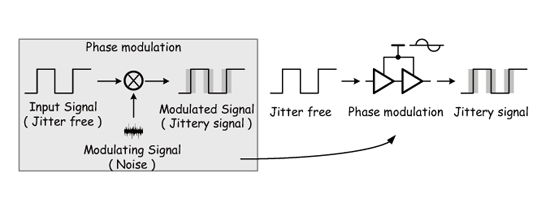
《图十九 模拟验证用之抖动产生示意图》
周期对周期抖动系统观察
为了确保整体系统操作正确性,接着我们将实际输入周期对周期抖动至系统中,藉此观察其操作特性。而周期对周期抖动的产生方式,我们将采用讯号调变法来实现,如图十九所示。其包含一个干净的参考时脉(input signal)、一个作为干扰源的调变讯号(modulating signal)和相位调变电路(phase modulator),藉由杂讯去改变理想时脉转态点实现抖动产生。
而以电路面来看,其实相位调变电路就是可调整电源电压的多级缓冲器。当一理想时脉进入缓冲器后,会有延迟产生,而延迟量和电源电压有极大关连性。电压越大延迟越小;反之电压越小延迟就会越大。利用此关系,我们只要将抖动做为缓冲器电压,就可以得到随着抖动变化的时脉相位。
抖动数位化观察
为了验证此系统是否能正确地把输入抖动数位化,因此我们也将利用两种不同型态之抖动来验证:一为正弦抖动、另一为振幅调变抖动。如图二十和二十一所示的抖动量数位化之模拟结果。从中可以得知,相关系统可成功依输入抖动型态运算出对应数位码,我们只需将数位码对照抖动表,即可得知输入抖动量。
《图二十 正弦抖动经抖动测试系统之输出结果》
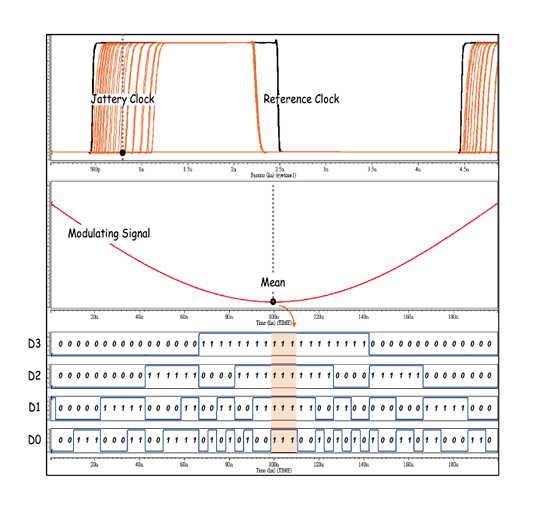
《图二十一 调幅抖动经抖动测试系统之输出结果》
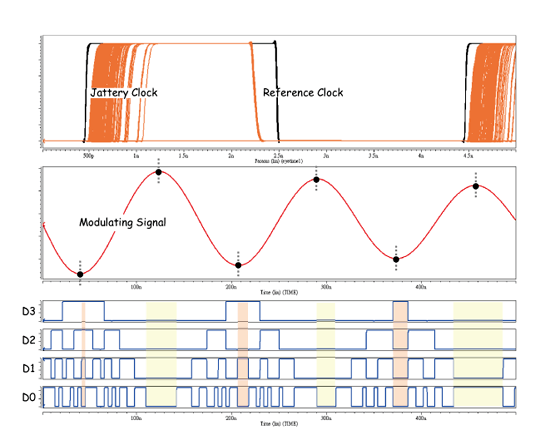
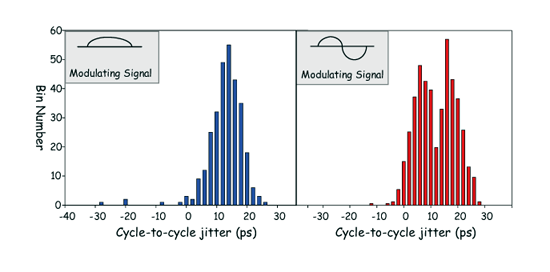
抖动测试准确度和测试时间关联密切,在足够测试样本下才能确保所得数值具备公信力,在测试时就必须让系统做长时间累计。我们将测试前述两种型态之抖动分布,此时系统会送出许多测试数值;而为了得知其真实抖动分布的情况,因此我们累加所有抖动量分布次数,其测试结果如图二十二所示。
抖动数值对应分析
经过长时间运算后,在半周期正弦抖动部份,图二十二左明显可看出其为一高斯分布,具有一个峰值,此值就落于正弦抖动的最大值上。而右图振幅调变抖动之测试结果,则显示双峰之抖动分布,且其双峰的分布量也不尽相同。这是因为振幅调变讯号每个峰值电压不同,而不同的峰值会对应到不同的数位码,所以在长时间抖动测试下才会出现此分布情形。
藉由以上的说明可得知,我们所提出之抖动测系统不但可以成功量化抖动量,并可藉由长时间的分析,可进一步地得知抖动分布型态,更可从中运算出抖动峰值、抖动均方根植、n倍sigma的抖动分布量…等等。
《图二十二 长时间累计抖动运算结果》
所提出测试法之测试结果
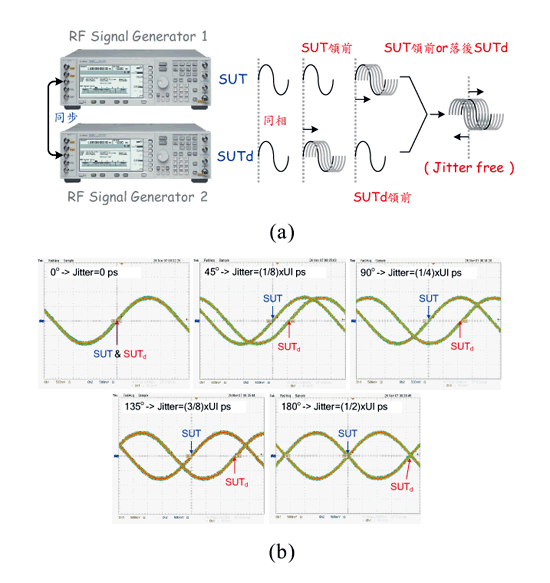
《图二十三 抖动产生示意图与实际测试图》
利用宽频抖动测试讯号
在量测环境的建构上,我们可分为两个部份:一为针对抖动放大电路作测试,另一则为全系统测试。在先前架构说明中提到,我们所提出的测试架构是针对待测讯号之周期对周期抖动作测试,因此需要一延迟电路,将每个周期讯号与延迟一个周期时间之讯号萃取出来。但为了要验证抖动放大电路操作特性,我们也需要一非常宽频与宽范围抖动测试讯号,因此采用图二十三的测试法。
亦即我们利用两台高频讯号产生器,分别产生代表SUT与SUTd之待测时脉讯号,因为时脉已强制同步,所以若不改变任何参数时,SUT与SUTd之讯号将保持同相位。而为了测试抖动放大电路的放大特性,可藉由调整其中一台讯号产生器之延迟量,来仿造实际时脉抖动情形。
如图中可以观察出,若调整讯号产生器2的延迟量,可实现落后抖动分量;若调整讯号产生器1的延迟量,则可实现领前抖动分量,藉此调整将可达到宽抖动范围之测试。此外因讯号产生器可产生大范围频率调整,所以也可进一步测试抖动放大器线性度。
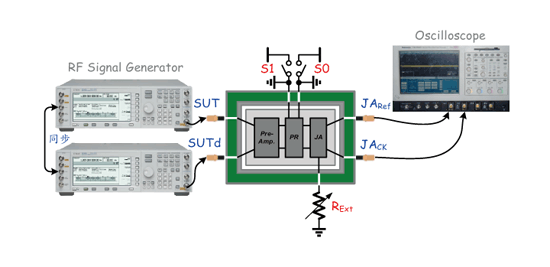
《图二十四 抖动放大电路量测环境示意图》
分析测试过程
图二十四为抖动放大电路测试环境示意图,其输入讯号为前述两台讯号产生器所提供之讯号。于晶片中前端会先有预先放大器(pre-amplifier)将输入转换为方波,随之送入脉波吞噬电路与抖动放大电路中。当抖动量经电路放大后,我们利用示波器来观测输出讯号间的相位差,再将输出相位差(JACK-JARef)除以输入相位差(SUT-SUTd),即可得到抖动放大电路之放大倍率。
此外当输入讯号频率改变时,可藉由调整S1和S0来选择较为适当的脉波吞噬数;而若当抖动放大电路于制作时发生漂移,则可藉由调整外部电阻RExt进而改变电流量,以确保抖动放大量的准确性。因此由以上所述之方法,将可测试出抖动放大倍率之线性度(JitterIn vs. JitterOut)、操作频宽(频率 vs. 放大倍率)与放大倍率和脉波吞噬数间的关系。
《图二十五 抖动量测系统之量测环境示意图》
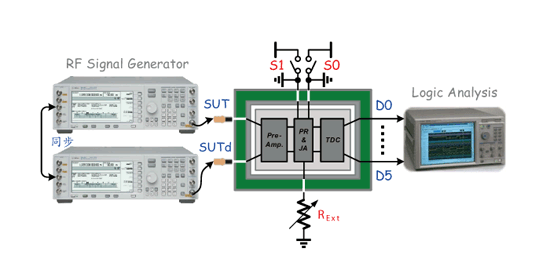
抖动量测环境分析过程
另外图二十五为抖动量测试系统之量测环境示意图。其前端和图二十四做法一致,但因抖动放大电路后接上时间-数位转换电路,因此已将抖动量化成数位码,所以我们藉由逻辑分析仪(Logic Analysis;LA)来运算即时输出之数位码;经一段有效时间运算后,再把逻辑分析仪所输出之结果与输入抖动量相比较,即可得知所提出之系统准确度。
《图二十六 输入抖动与输出抖动之量测图:随着箭头方向代表输入抖动递增》
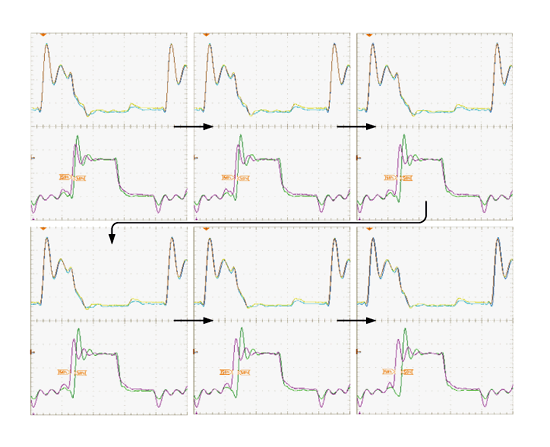
首先,我们将所提出的抖动放大电路,使其操作在不同输入抖动量下,观察放大倍率间的变化,如图二十六所示。为了测试纪录方便,我们采用6个测试pattern来验证,也就是说利用6个不同的输入抖动量送入抖动放大电路中,然后量测输出抖动量,以绘出抖动放大曲线图。此外为了验证我们所提出的脉波吞噬观念可修正放大线性度,所以也针对四个频段做验证。
《图二十七 抖动放大倍率vs.操作频率》
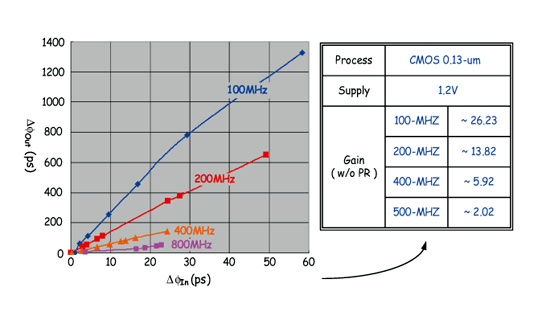
抖动放大电路测试结果
图二十七即为抖动放大电路测试结果。从图中可观察出,在低频操作时,因为稳态区域足够,所以其输出抖动与输入抖动比,与当初所设计的相距不远。但随着待测讯号频率上升、稳态区间缩小,在不调整脉波吞噬数目的条件下,放大倍率会随之缩小,甚至放大倍率消失,导致系统操作错误。以800-MHz的条件为例,此区段放大倍率已下降至约2倍左右,此时已完全无法弥补时间-数位转换电路解析度不足的缺点。因此从此测试可观察出,虽于各频段内放大倍率皆可维持放大倍固定,但只要输入讯号频率一变化,就会造成放大倍率失真以至于会有误判的情形。因此接下来将依前述的说明适当切换脉波吞噬数,来达到宽频之放大倍率。
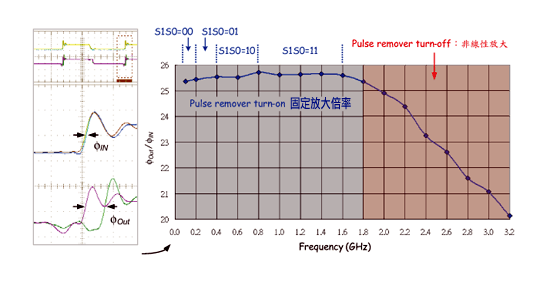
如图二十八所示,在不同频段操作下我们去改变脉波吞噬的数目,也就是切换S0、S1,让抖动放大电路在不同频段下皆具有足够宽的稳态区间。此外也藉由调整外调电阻将抖动电路之放大倍率作些微的修正。图中显示经调整脉波吞噬数后,于数十MHz~1.6GHz附近其放大倍几乎维持在25.5倍左右。但若超过1.6GHz后,因为tfn时间点慢慢靠近ts造成稳态电位的变化,所以放大倍率开始有些许改变。操作频率继续往上升,tfn点会等于或是超前ts,造成放大倍率急速下降,所以说此抖动放大电路的线性放大区为数十MHz~1.6GHz。在此必须说明因为线性区间可藉由改变脉波吞噬的数目来达成,因此若须操作在更高频的运用上时,我们只需依造(2)式来实现即可。
《图二十八 放大倍率与频率间之关系图》
《图二十九 多工式振荡器之振荡频率测试图》
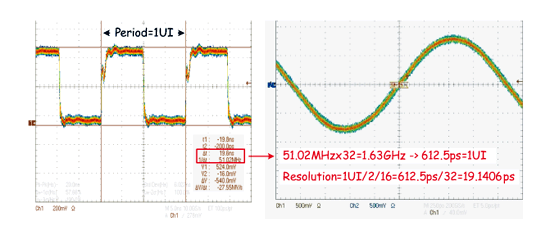
时间-数位电路最佳解析度
除了抖动放大电路测试外,时间-数位转换电路也关系到系统最佳解析度。因此也藉由调整输入抖动量来观察数位输出码,并测试多工式振荡器振荡频率来回推解析度。如图二十九所示,为了测试方便,我们将振荡频率除以32来观测,所以此时间-数位转换电路的最佳解析度,为振荡周期除上32个相位(经内插后所得),亦即约为19-ps。
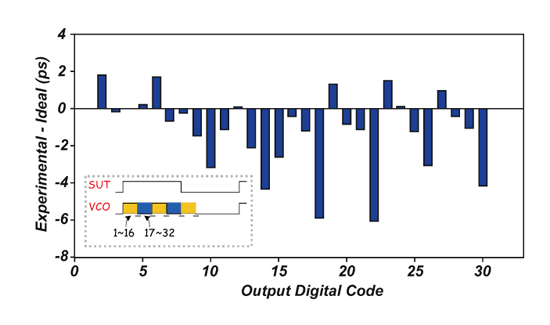
此外图三十为输入抖动量与数位输出码之对照图。其显示输入抖动每增加19-ps数位码也随之增加,但量测曲线与理想曲线间相差约40-ps。此误差量来自于振荡器之抖动。但以系统层面来看,我们只要将此误差量扣除即可,因为其所关心的是每个数位码间所代表的抖动量是否相同,因此我们将图三十误差量归零后进行积分非线性误差量(Integral Nonlinearity;INL)之分析,如图三十一所示。此时间-数位转换电路最大偏移量约为6-ps,即0.32LSB(1LSB=19-ps),其小于0.5LSB,所以可说对于系统操作时并不会带来严重的错误。
《图三十 输入抖动 vs. 数位输出码》
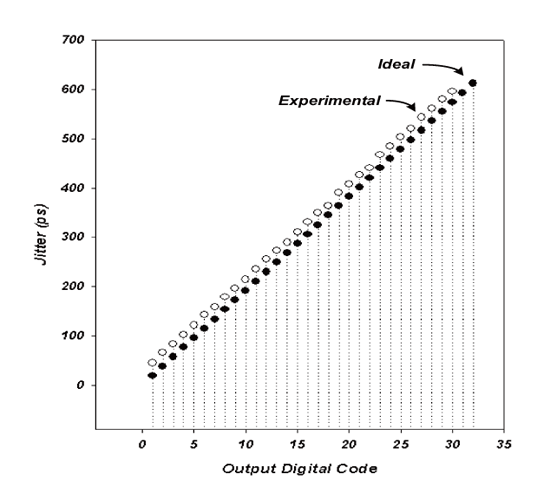
《图三十一 时间数位转换器之INL分析图》
得出系统解析度
确定了抖动放大电路与时间-数位转换电路操作特性后,接着我们将可推得系统解析度。因为放大倍率A与延迟单元之延迟时间的比例为25.5:19,所以在此条件下所能测到的最佳解析度即为19-ps/25.5=0.8-ps。同理可证,若在设计上将倍率提升或是缩小延迟时间至其比例为1:2时,此将可把解析度进一步提升至0.5-ps。有鉴以上量测与模拟之结果,我们可以说此测试方法将可成功运用在wide range以及low jitter的内建时脉抖动测试架构中。
结语
在先前所列举的五种传统测试架构,不外乎是利用电路技巧来缩小延迟单元的延迟时间,以等效增加测试解析度。然而当测试速度上升或是抖动量来到sub-ps等级后,因电路与制程上之瓶颈,其所能量测的范围皆会受到限制。
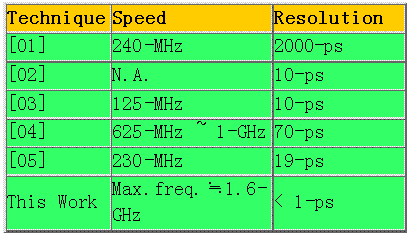
基于上述之原因,本文提出不同于传统测试架构的测试策略。这是采用抖动放大的观念,先针对待测讯号抖动量做先期放大,然后利用时间-数位转换电路将抖动量化,再把得到的输出数位码除以放大倍率,即可还原出原本的周期对周期抖动量。此外为了让此测试架构能操作在任何频段下,因此还采用单撷取搭配脉波吞噬的测试方法,拉长抖动放大时的稳态时间,以得到固定放大倍率,进而减少因频率变化所带来的量测误差。所以本文所提出方法相较于传统测试方式,将具备宽频操作、低抖动量测试、高解析度、成本低、受测试环境限制程度小等优点。最后其比较如表三所示。
(表三) 各种架构比较表
(完)
(转自工研院系统晶片科技中心技术期刊第8期。作者李瑜和郑乃禛)