郭子逸1 郑卫刚2
【摘 要】根据卡尔曼滤波原理以及柴油机缸内压力信号的特点,应用MATLAB软件设计了一个卡尔曼滤波器,通过反馈滤波误差协方差的大小,来改变滤波器算法中的测量系统误差的大小,使滤波效果更准确。通过对比滤波前后示功图及幅频图,结果表明,该滤波器较好地兼顾了滤波稳定性及估计精度。
关键词:卡尔曼滤波,幅频图,柴油机缸内压力信号
A Study on Kalman Filtering diesel cylinder pressure signals
with Matlab
Guo ziyi1 Zheng Weigang2 Zheng Xiaolu1
(1 Department of Energy and Power Engineering, WHUT;2Engineering Training Center, WHUT;)
Abstract Based on the principles of Kalman filter and the characteristics of diesel cylinder pressure signals, a Kalman filter is established with MATLAB software. Systematic errors in filter algorithm will be changed with the filtering error covariance for a more precise result. Comparing indicator diagram and amplitude frequency diagram before and after filtering, the results show that the Kalman filter is stable and precise.
Key words:Kalman filter; amplitude frequency diagram; diesel cylinder pressure signals
引言
内燃机示功图是深入研究内燃机工作过程和动力性能指标的重要手段,准确提取示功图、有效去除示功图中各种误差时整个分析工作的基础,是获得准确分析结果的根本保证。但是精确的示功图得到是比较困难的,一般认为影响示功图测量精度的主要因素有测压通道效应以及燃烧造成的对压电传感器的热冲击效应。在示功图测试中,将传感器与燃烧室壁面平齐安装方式虽然可以避开通道效应,但是此时传感器的热冲击效应大大加强,膨胀冲程的压力测量值严重失准;并且传感器的热负荷很高,易于损坏;同时在很多结构紧凑的柴油机没有足够的空间来平齐安装传感器。因此内燃机示功图的侧量难免带来许多误差。
数据光顺是数据处理中比较常用的纯数学方法,但缺乏客观物理模型的支持,因而缺乏光顺性和客观实际逼近的评价标准,无法证明平滑过的示功图是否切合实际。随着数字信号处理理论与应用发展,人们目前一般对采集到时域信号经过傅里叶变化得到频域信号,即对测量得到的气缸压力信号进行频谱分析,得到气缸压力的频谱特性。一般将频域区域划分为低中高三个频域,目前一般认为通道效应的主要影响于示功图的中频域,然后对中频域端幅值取零,再通过傅里叶逆变换将修改后的频域信号转化为时域,即为滤波后的信号图。但是许多文献对这种方法没有令人信服的说明,因而对示功图进行滤波处理缺乏说服力[1]。
本文基于自动控制理论中最经典理论之一卡尔曼滤波理论,应用matlab软件,直接对测量得到的缸内压力信号图,即时域信号进行滤波,省去了使用傅里叶正逆变换将时域与频域来回转换的步骤。并且卡尔曼滤波经过多年的改进与应用这一理论已经成熟,在各个领域也有了比较多的应用。
示功图滤波国内外现状
本质上来讲,滤波就是一个信号处理与变换(去除或减弱不想要的成分,增强所需成分)的过程,这个过程既可以通过硬件来实现,也可以通过软件来实现。在实际示功图的测录过程中,常有一系列因素影响着示功图本身的准确性,例如上止点的偏差、测压通道的腔振等。
基本Kalman滤波原理
卡尔曼滤波由于其在求解时不需要贮存大量的观测数据,并且当得到新的观测数据时,可随时算得新的参数滤波值,便于实时地处理观测成果,因此,卡尔曼滤波被越来越多地应用于动态数据处理中。
卡尔曼滤波基本思想是:以最小均方误差为最佳估计准则,采用信号与噪声的状态空间模型,利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计,求出当前时刻的估计值,算法根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误差的估计。
图 1 Kalman滤波算法框图
从建立的系统数学模型出发,可以导出卡尔曼滤波的计算原型。为了便于描述,做以下说明:(1),第k步之前的状态已知的情况下第k步的先验状态估计值(-代表先验,^代表估计);(2),测量变量Z(k)已知情况下第k 步的后验状态估计值[6]。
先验估计误差的协方差矩阵为:
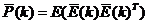
(1)
后验估计误差的协方差矩阵为:
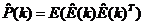
(2)
式(3)构造了卡尔曼滤波器的表达式:先验估计和加权的测量变量Z及其预测之差的线性组合构成了后验状态估计:
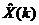
.png)
(3)
式中测量变量及其预测值之差反映了预测值和实际值之间的不一致程度,称为测量过程的残余。n×m阶矩阵K叫做残余的增益,作用是使后验估计误差协方差最小。可以通过以下公式求出K:
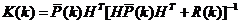
(4)
对卡尔曼增益K的确定是建立滤波模型的关键步骤之一,它能显著影响模型的正确性和效率。
单步预测误差协方差矩阵:
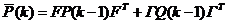
(5)
滤波误差协方差矩阵:
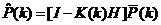
(6)
其中,,,为系统过程噪声向量,为系统误差,为观测噪声向量,为观测误差。
需要指出的是,可以看作Kalman滤波的性能评价,因为
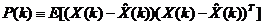
(7)
实际上,式(6)是由式(7)推导得到的。
滤波增益:

(8)
单步预测误差协方差矩阵:
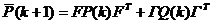
(9)
实际计算时,对于k+1步而言,总是假设前一时刻k时刻的和是已知的,那么就先根据式(9)求,将代入式(8)求出,再分别根据式(3)和式(7)求出和。到了k+2时刻,如法炮制。对于和一般的处理方法为,假定,而是一个正定矩阵即可,一般可以令其为一个对角阵,其对角元素的数值较大,即为一个对称正定阵。在此条件下,Kalman滤波的可观性与可控性条件一般可以满足,滤波是收敛的。
应用matlab构造带反馈的Kalman滤波器
卡尔曼滤波器是一个最优化自回归数据处理算法,它的广泛应用于航空器轨道修正、机器人系统控制、雷达系统与导弹追踪等。近年来更被应用于组合导航与动态定位,传感器数据融合、微观经济学等应用研究领域。特别是在图像处理领域如头脸识别、图像分割、图像边缘检测等当前热门研究领域占有重要地位。
本文在处理柴油机压力测量信号时,根据柴油机缸内压力信号的特点以及卡尔曼滤波的性能,本文设计的卡尔曼滤波器是基于随机线性离散系统卡尔曼滤波的基本方程,这类型的滤波方法不仅适用于平稳序列的滤波,而且也适合于非平稳的滤波。
由试验与信号测试数据采集技术等相关知识可以得到,当测量值比较小或测量范围波动较小时,测量系统的误差(即上节所描述的)相对来说比较大;相反的当测量值比较大或测量范围波动较大时,测量系统的误差相对来说比较小,测量系统的误差(即上节所描述的)相对来说比较小。如果滤波器全程只采用一个系统误差,当选用的系统误差较小时,如时,如图,进排气冲程滤波效果比较理想,然而压缩以及燃烧做工阶段滤波后的示功图有明显的偏差。
图 2 系统误差较小时卡尔曼滤波效果对比图
然而,当选用的系统误差较大时,如时,如图,压缩以及燃烧做功阶段原始信号图就比较光滑,滤波后效果比较逼近原始值,效果较好。然而进排气冲程滤波后的示功图仍然保留着原始信号中的大量噪声及误差信号,没达到理想的滤波效果。
图 3 系统误差较大时卡尔曼滤波效果对比图
因此,考虑到柴油机缸内信号波动范围比较大,在柴油机进气和排气冲程中的压力变化不大,基本上与角度值呈线性关系;然而在内燃机压缩行程和燃烧膨胀冲程时压力经历了骤增骤减的一个过程,与角度值呈非线性关系。因此滤波器设计时主要考虑这方面因素,在角度值处于进气和排气冲程时,选用;在压缩冲程以及燃烧做功冲程中,选用。最终经过卡尔曼滤波器滤波后的示功图与原信号图对比,如下图,可以看出,经过卡尔曼滤波器滤波后的示功图去掉了原始信号图中的很多“毛刺”,更加光滑,尤其在进气和排气阶段;而在压缩以及燃烧做工阶段,由于原始信号图就比较光滑,滤波后的示功图也比较逼近原始信号。总的来说,整个示功图滤波效果既保留了原始有用的信号,又将大量噪声信号进行了滤除。
图 4 动态改变系统误差时卡尔曼滤波效果对比图
将卡尔曼滤波前后的示功图数据进行傅里叶正变换,将原始的时域信号转变为频域信号,如图5。由于噪声信号通道效应等测量示功图时的干扰信号主要存在于高频部分,因此如果幅频图的高频成分越小,则说明其对应示功图的信号越纯正。可以清楚地可以看出,本文设计的滤波器清楚地滤掉了100HZ以后的高频成分,因此图4的滤波后示功图相比原始图更加光顺。从频域上来分析100HZ以后的高频成分的波动减弱。说明本文设计的滤波器消除了一些高频干扰信号,滤波器基本准确合理。
图 5卡尔曼滤波前后幅频图
结束语
(1) 根据柴油机缸内信号在不同冲程中波动范围不同反馈不同系统误差,在柴油机进气和排气冲程中的压力变化不大,基本上与角度值呈线性关系,系统误差选用;然而在内燃机压缩行程和燃烧膨胀冲程时压力经历了骤增骤减的一个过程,选用。这样设计出来的卡尔曼滤波器使得整个信号曲线滤的比较光滑,去掉了很多“毛刺”,保留了大量有用的信号,效果较好。
(2) 通过对比滤波前后示功图及幅频图,实验结果表明,本文所设计的滤波器精度较为理想,比较可靠。
参考文献
侯玉春,黄震,李德钢,罗马吉. 发动机缸内压力信号频谱分析及滤波方法的研究[J]. 振动与冲击. 2005
何学良,李疏松. 内燃机燃烧学[M]. 北京:机械工业出版社. 1990.
彭勇,周轶尘. 应用小波变换法分析内燃机示功图[J]. 武汉交通科技大学学报. 1998.
朱建元. 示功图测压通道的固有频率估计及数字滤波[J]. 内燃机工程. 1998.
石磊,刘琳,王月,吴波. 利用广义频率抽样滤波法处理振荡示功图[J]. 山东内燃机. 2003.
王翼. 现代控制理论[M]. 机械工业出版社. 2005.1.
付梦印,邓志红,张继伟. Kalman滤波理论及其在导航系统中的应用[M]. 科学出版社. 2003.10.