肖振中 梁晋 于德弘 唐正宗
(西安交通大学机械工程学院,西安710049)
摘 要:。
关键词:光学测量;近景摄影测量;光束平差;相机自标定
中图分类号: TP393 文献标识码:A
Study on the Technologies of Rapid Three-dimension Optical Measurement for Key Points on Large Complex Components
XIAO Zhenzhong LIANG Jin YU Dehong TANG Zhengzong
(School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China )
Abstract :.
Key words:Optical Measurement;Close Range Photogrammetry;Bundle Adjustment;Camera Self-Calibration
1 引言
。
2 关键技术
1)标志点检测
在开始测量前首先要在被测工件上粘贴标志点,测量的过程就是通过所拍摄的工件表面多个位置的图像重建出标志点的三维坐标。本文使用两种圆形标志点,如图1所示,黑底白色圆点和带有环形编码的圆形标志点。

图 1 标志点图案
使用圆形标志点可以获得比较高的检测精度,带有环形编码的标志点则可以方便的实现同名点的匹配,用来实现相机姿态自动化定向。圆形标志点在经过投影后在图像上呈椭圆形,标志点检测流程见图2。首先将获取的图像转化为8位灰度图像;然后使用Canny算子进行边缘检测;在结果中搜索可能的椭圆边界,同时排除不可
Canny边缘检测搜索椭圆粗边缘亚像素椭圆边缘修正最小二乘拟合椭圆遍历一周编码环存在该编码值非编码标志点编码标志点否是
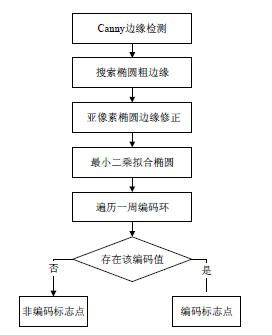
图 2 标志点检测流程图
能的边缘;对确认为椭圆边界的图像点使用梯度均值法进行亚像素修正,然后使用最小二乘法拟合得到椭圆中心和长短轴、旋转角等信息;最后以该椭圆为中心,在其外围对原始灰度图进行灰度采样,得到编码环的编2
码,如果存在该编码值,则认为是编码标志点,否则为非编码标志点。
2)相机姿态自动定向
每一个相机姿态包含投影中心位置S(X,Y,Z)和像平面姿态角(ω,ψ,κ)共六个元素。相机姿态定向就是确定每一幅图像这六个外方位元素的过程,分相对定向和绝对定向两种。确定两幅图像相对方位的过程叫做相对定向;确定一幅图像在物方坐标系中的绝对方位的过程叫做绝对定向。相机姿态定向是光学测量的基础,精确的相机姿态自动定向也是光学测量的难点。本文使用环形编码标志点实现相机姿态的自动定向,具体流程如下:
① 对所有图像逐一进行标志点检测,编码标志点要检测出相应的编码环数值;
② 搜索包含6个以上公共编码标志点的两幅图像,根据公共点的数量对搜索结果排序;
③ 对搜索结果中第一组的两幅图像进行相对定向,如果定向不成功则换下一组图像继续进行相对定向;
④ 两幅图像相对定向成功后,以其中一幅图像投影中心为坐标原点建立坐标系,重建出公共编码标志点的三维坐标;
⑤ 在未定向的图像中搜索包含6个以上已重建标志点的图像,使用直接线性变换(DLT)方法进行绝对定向,定向成功后,再重建出该图像与其它已定向图像中未重建的公共编码标志点;
⑥ 重复步骤⑤,直到没有新的图像可以被定向为止;
经过以上六个步骤,就可以实现相机姿态的自动定向。相机姿态绝对定向采用直接线性变换(DLT)的方法求解,该方法属于线性解法,至少需要6个公共点,在其他文献中有详细论述,本文不作详细介绍。
相机姿态相对定向,如图3所示,S1-xyz为图像1相机坐标系,S2-x’y’z’为图像2相机坐标系,S2-xyz为与S1-xyz平行的辅助坐标系。S1S2与平面S1xy夹角为v,S1S2在平面S1xy的投影与坐标轴S1x夹角为u。假设物方点P在图像1中对应的像点p1在S1-xyz坐标系坐标为(x1,y1,-f),物方点P在图像2中对应的像点p2在S2-x’y’z’坐标系坐标为(x2’,y2’,-f),p2在S2-xyz坐标系坐标为(x2,y2,z2),
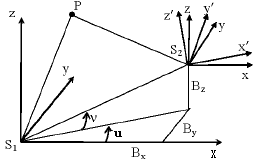
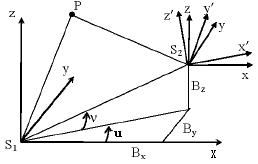
图 3 相对定向示意图
S2在S1-xyz坐标系坐标为(Bx,By,Bz),假设S2-x’y’z’与S2-xyz坐标系旋转矩阵为R,因为S1p1、S2p2、S1S2的共面关系,则有:
(1) ....−....fyxRzyx'2'2222
(2) 022211=−zyxfyxBzByBx
其中:
By=Bx*tg(u)≈Bx*u;
Bz=Bx*tg(v)/cos(u) ≈Bx*v;
因此公式(2)可以简化为:
(3) 0222111=−zyxfyxvu
由公式(1)和(3)可以看出只要两幅图像存在5个以上公共点就可以求解其相对方位(u,v,R)。
3)光束平差法与相机自标定
基于共线条件方程的摄影测量光线束平差解法(Method of Bundle Adjustment),是一种把控制点的像点坐标、待定点的像坐标以至其他内业、外业量测数据的一部分或全部均视作观测值,以整体地同时地求解它们地或是值和待定点空间坐标地解算方法。其求解原则是使各类观测值地改正数V满足VTPV为最小[3]。所谓的相机自标定就是指将相机内、外参数放在一起同时进行整体平差计算,也就是带有附加参数的整体光束平差。本文的光束平差中将相机内参数、相机外参数和物方点世界坐标均作为观测值参与优化。基于共线方程列出光束平差的误差方程:
(4)LXCXBXAV−+=3*2*1*3
其中:X1为摄像机内参数变化量;X2为摄像机外参数变化量;X3为三维坐标变化量;L为观察量即图像点坐标;A、B、C分别是相应的变化量偏导矩阵。
在光束平差时全面的考虑了相机镜头的径向畸变、切向畸变和薄棱镜畸变,以降低重投影误差,提高了自标定精度。光束平差时使用的畸变模型[6][7]:
(5) yExEByxxrBrxArxArxAdx*2*12***2)2(*1**3**2**122642+++++++=
(6) 1***2)2(*2**3**2**122642ByxyrBryAryAryAdy+++++=
其中:A1、A2、A3为径向畸变参数;B1、B2为切向畸变参数;E1、E2为薄棱镜畸变参数。
4)非编码标志点匹配、重建与厚度校正
标志点的匹配就是在多个图像中寻找同一个物体点对应的像点的过程。立体匹配在计算机视觉中是极为重要的难题之一,由于受光照条件、噪声信号干扰、镜头畸变等诸多因素影响,空间三维目标被投影到二维图像时,在不同的视角下可能会有较大不同。摄影测量中常用的匹配算法有最小二乘匹配、基于特征的匹配、和灰度相关匹配等等。对于带有环形编码的标志点由于具有唯一标识的编码可以方便的利用其特征编码进行立体匹配。然而,对于没有编码的圆形标志点的正确匹配就成了难题。基于外极几何关系的匹配算法在双目立体视觉因只能推断出匹配结果在外极线上,匹配歧异性较大而影响其广泛应用。近景摄影测量中存在多个相机位置,利用多个图像上的外极线约束就可以大大提高非编码标志点匹配的正确率,见图4。
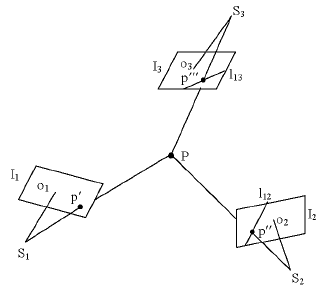
图 4 多图像外极线匹配示意图
非编码标志点匹配策略如下:
① 图像S1中标志点P’在图像S2中对应点在外极线l12上,将图像S2中符合条件的标志点记录到点集Q12中;
② 图像S1中标志点P’在图像S3中对应点在外极线l13上,将图像S3中符合条件的标志点记录到点集Q13中;
③ 点集Q12和Q13中的满足图像2和图像3对应的外极关系的点才可能是图像1中标志点P’对应的像点,如果满足外极关系的点对只有一对,则认为匹配成功,如果仍然出现多个点对,则继续使用另外的图像加以判别;
通过实际的匹配实验验证,在图像质量较好的条件下,匹配正确率达99%以上。
在正确获得了非编码标志点的匹配像点后就可以通过相机内、外参数重建出该点的三维坐标和标志点平面法向量。因为标志点本身具有一定的厚度(约0.1mm),所以我们所重建出的标志点三维坐标并不是工件表面的真实坐标,利用重建得到的标志点平面法向量则可以去除标志点厚度带来的误差,得到真实的工件表面三维坐标。
3 实验与分析
三维光学快速检测系统软件在VC++6.0下开发,运行环境为WindowsXP系统。硬件由单反数码相机NIKON D200、环形闪光灯、磁性环形编码标志点、十字方向尺和定长标尺组成。单反数码相机CCD尺寸为:23.6cm×15.8cm,像素大小:6.09um×6.09um,分辨率3872×2592;光学镜头采用尼康焦距20mm定焦镜头。如图5所示,拍摄范围约1-5米,使用外置环形闪光灯,保证图像各部分亮度均衡,获得较高的图像质量。

图 5 三维光学快速检测系统组成4
以3米×3米×1米大型水轮机叶片为被测对象,见图6,在其表面布置环形编码标志点和非编码标志点。

图 6 水轮机叶片
为验证系统测量精度,对水轮机叶片进行七次测量,选取其中五个点对之间距离作为考察对象,同时,使用德国GOM公司工业近景摄影测量系统Tritop也进行七次测量,对比
4 结论
参考文献
[1] Mignosi,A;Touron,G;ModelDeformation Measurement in the ONERA F1 Wind tunnel[J].Instrumentation in Aerospace Simulation Facilities,2007:1-8.
[2] C.C.Chang,Y.F.Ji. Flexible Videogrammetric Tech- nique for Three-Dimensional Structural Vibration Measurement[J].Journal of Engineering Mechanics, Vol.133,No.6,June 1,2007.
[3] Zhengyou Zhang. A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,VOL. 22,NO. 11,NOV 2000.
[4] Thomas Luhmann.Close Range Photogrammetry[M]. 2000.
[5] Reza Hassanpour,Volkan Atalay. Camera auto- calibration using a sequence of 2D images with small rotations[J].Pattern Recognition Letters,2004:989-997.
[6] Clive S.Fraser. Digital camera self-calibration [J].Photogrammetry & Remote Sensing,1997:149-159.
[7] Sheng-Wen Shih,Yi-Ping Hung.Calibration of an Active Binocular Head[J]. IEEE Transactions on System,man,and Cybernetics-Part A: Systems and Humans,VOL. 28,NO. 4,JULY 1998.
作者简介:肖振中(1980-),男,山东济宁人,博士研究生,主要研究方向:三维光学测量; 梁晋(1968-),男,河南郑州人,副教授,博士,主要研究方向:三维光学测量;于德弘(1949-),男,山西太原人,教授,博导,主要研究方向:模具设计与检测; 唐正宗(1982-),男,山东日照人,硕士研究生,主要研究方向:数字图像处理