当我们用光谱仪进行测量时,我们希望相信所获得的结果。无论我们测量成分或厚度,无论我们采用XRF、OES或LIBS进行分析,我们都希望所获得的结果尽可能准确。
信任我们的测量结果的第一步是理解我们对准确性的定义。
准确性定义
在光谱学中,准确性是衡量我们的测量值与期望值有多接近的尺度。(我们希望期望值是真实值,但由于我们无法知道真实值,因此我们使用期望值这个术语。)
准确性取决于两个因素:
下图说明了精密度和正确度如何共同影响准确性。
.png)
由此可知,有可能获得良好精密度,但也有可能获得差的正确度。并且有可能获得高正确度(平均值的准确性)和差的精密度。为获得真正准确的结果,我们既需要高精密度又需要正确度。
不同的误差类型
在解决我们希望减少的误差之前,我们应该先讨论我们想要消除的误差。
过失误差
我们的首要任务是检查并消除测量中的过失误差。通过观察上述图表,我们会发现,一个过失误差将导致测量结果完全位于绿色区域之外,并且可能会被视为异常。制备过程中的样品污染等工艺误差可能导致过失误差。缺陷样品亦如此,例如,测量区域中的空腔或运行不正确的测量程序也会导致过失误差。通过培训和使用正确的程序,可以避免过失误差。
我们必须假设测量系统中存在两种误差类型:
系统误差通常与正确度有关,并在测量样品的平均值和预期结果之间给出一致的偏差。造成这类误差的原因在于设备缺乏维护、部件磨损或校准不良等设备故障。由于偏差对于确定的关注区域内的每个测量值均一致,因此可以测量偏移量,然后将校正系数合并到样品测量值中。定期校准和维护可以减少系统误差。
随机误差与精密度有关。随机变化越大,测量精密度越低,误差幅度越大。不同于系统误差,这类误差是不可预测的,并且使用统计方法进行估计。这些测量波动可能由样品的不均匀性、测量环境的微小变化以及用于校准的参考样品的测量不确定性造成。目标是通过良好的程序和维护良好的设备,尽可能提高精密度。
如何获得您信任的结果
事实上,您能完全相信结果的唯一方法是您了解读数的误差范围。在每次测量中,由于测量系统的局限性和其中的随机波动,总会存在误差范围。为获得尽可能准确的读数,我们应消除过失误差,减少系统误差和随机误差,然后在商定的置信度内接受并计算剩余的误差范围。
从本质上讲:在置信度为95%的情况下,铬成分为20%+/-0.2%,这是一个值得信赖的结果。而这种说法:铬成分为20%,是不完整且不可靠的结果。
可通过简单的计算来确定系统误差(平均值偏移)。随机误差遵循统计学模型。我们将在指南“探索真值”中向您展示如何计算这两种类型的误差。请点击“阅读原文”下载指南。
.gif)
销售热线:400 621 5191
服务热线:400 622 5191
当我们用光谱仪进行测量时,我们希望相信所获得的结果。无论我们测量成分或厚度,无论我们采用XRF、OES或LIBS进行分析,我们都希望所获得的结果尽可能准确。
信任我们的测量结果的第一步是理解我们对准确性的定义。
准确性定义
在光谱学中,准确性是衡量我们的测量值与期望值有多接近的尺度。(我们希望期望值是真实值,但由于我们无法知道真实值,因此我们使用期望值这个术语。)
准确性取决于两个因素:
下图说明了精密度和正确度如何共同影响准确性。
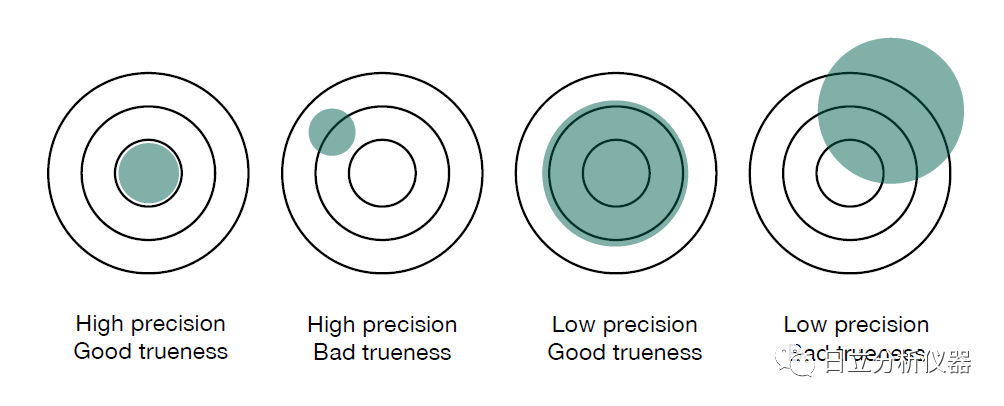
由此可知,有可能获得良好精密度,但也有可能获得差的正确度。并且有可能获得高正确度(平均值的准确性)和差的精密度。为获得真正准确的结果,我们既需要高精密度又需要正确度。
不同的误差类型
在解决我们希望减少的误差之前,我们应该先讨论我们想要消除的误差。
过失误差
我们的首要任务是检查并消除测量中的过失误差。通过观察上述图表,我们会发现,一个过失误差将导致测量结果完全位于绿色区域之外,并且可能会被视为异常。制备过程中的样品污染等工艺误差可能导致过失误差。缺陷样品亦如此,例如,测量区域中的空腔或运行不正确的测量程序也会导致过失误差。通过培训和使用正确的程序,可以避免过失误差。
我们必须假设测量系统中存在两种误差类型:
系统误差通常与正确度有关,并在测量样品的平均值和预期结果之间给出一致的偏差。造成这类误差的原因在于设备缺乏维护、部件磨损或校准不良等设备故障。由于偏差对于确定的关注区域内的每个测量值均一致,因此可以测量偏移量,然后将校正系数合并到样品测量值中。定期校准和维护可以减少系统误差。
随机误差与精密度有关。随机变化越大,测量精密度越低,误差幅度越大。不同于系统误差,这类误差是不可预测的,并且使用统计方法进行估计。这些测量波动可能由样品的不均匀性、测量环境的微小变化以及用于校准的参考样品的测量不确定性造成。目标是通过良好的程序和维护良好的设备,尽可能提高精密度。
如何获得您信任的结果
事实上,您能完全相信结果的唯一方法是您了解读数的误差范围。在每次测量中,由于测量系统的局限性和其中的随机波动,总会存在误差范围。为获得尽可能准确的读数,我们应消除过失误差,减少系统误差和随机误差,然后在商定的置信度内接受并计算剩余的误差范围。
从本质上讲:在置信度为95%的情况下,铬成分为20%+/-0.2%,这是一个值得信赖的结果。而这种说法:铬成分为20%,是不完整且不可靠的结果。
可通过简单的计算来确定系统误差(平均值偏移)。随机误差遵循统计学模型。我们将在指南“探索真值”中向您展示如何计算这两种类型的误差。请点击“阅读原文”下载指南。

销售热线:400 621 5191
服务热线:400 622 5191