王中华1,2 曾智 1,2,3 张存林1,2黄新萍1,2

　　1首都师范大学物理系,北京市太赫兹波谱与成像重点实验室，北京100048

　　2首都师范大学物理系，太赫兹光电子学教育部重点实验室，北京100048

　　3重庆师范大学物理与电子工程学院，重庆400047

　　摘要 如今很多的红外检测定量分析方法，常以特征时间和缺陷深度的关系为基础，本文以预设6个平底洞的不锈钢作为实验试件，选取一种不需要参考区域的PSDT法进行测厚计算。以对数温度曲线的二阶微分峰值时刻作为特征时间，利用特征时间与深度的平方成正比关系，可达到测厚的目的。用VC软件编程实现任意点的数据计算，先用最小二乘多项式拟合数据再计算对数温度-对数时间的二阶微分峰值时刻，将结果用以图形直观精确地显示出来，最终实现了缺陷深度的自动测量。

　　关键词 二阶微分峰值;深度测量;红外脉冲检测

　　中图分类号：O434.3 文献标识码：A

　　The research of defect depth’s measurement based on the method of second-order derivatives peak value

　　Wang zhong-Hua1,2 Zeng Zhi1,2,3 Zhang Cun-Lin1,2Huang Xin-Pin1,2

　　1Department of Physics, Capital Normal University, Beijing key Laboratory for Terahertz Spectroscopy and Imaging, Beijing 100048，China

　　2Department of Physics, Capital Normal University, Key Laboratory of Terahertz Optoelectronics Ministry of Education, Beijing 100048，China

　　3Institute of Physics and Electronic Engineering, Chongqing Normal University, Chongqing 400047，China

　　Abstract Recently many methods of quantitatively analysis infrared evaluation have been proposed,which always based on the relationship between specified characteristic time and defect depth.In this paper,using a PSDT method to predict of defect depth,which do not need a reference.Stainless steel which was machined with six flat-bottom holes is selected as experimental sample.Second-order derivative of logarithmic temperature's peak time is specified characteristic time.Specified characteristic time has certain relation with square of defect depth.Using VC programming to compute any hole of the sample.Fitting the data by least squares polynomial,then compute logarithmic temperature-logarithmic time's second-order derivative peak time.The final results is showed by figures directly and concisely.So it realized the measurment of defect depth automatically.

　　Key words Peak value of second-order derivatives;Measurement of depth;Infrared pulsed thermography

　　0引言

　　目前红外脉冲无损检测技术已应用到各种材料缺陷的探测，通过主动地对物体施加周期、脉冲等函数形式的可控热激励热激励，使物体内部的缺陷以表面场温差表现出来，并使用热像仪连续观测并采集表面温场的变化，由此获得的热像图是继续分析的重要依据。定性定量地探测分析各类缺陷已有广泛的应用，例如复合材料和金属材料的腐蚀、碰撞损伤、分层等。诸多理论和实验证明脉冲红外热成像的定量研究在缺陷的深度、大小和热性能是有效的[2-3]。

　　在过去的20年里缺陷深度的定量测量已经成为重要的热门研究课题，很多的测厚方法也产生了，这也包括通过特征时间(SCT)来确定缺陷深度的方法。在一维或者二维传导模式下，进行分析得到某个峰值时间作为特征时间，特征时间的准确与否直接关系到测量结果的准确性。常用的测厚方法有热对比度峰值法(PCT法)，热对比度变化率峰值法(PST法)，对数温度-对数时间曲线分离法，对数温度-对数时间二阶微分峰值法(PSDT法)，前三种方法均需选取参考，参考的选取可以是无缺陷区域温度，或者是整个表面温度的平均作为参考温度，或者是前几帧的平均温度，利用热对比度(有缺陷区域的温度减去无缺陷区域的温度)峰值确定特征时间，PSDT法不会因为手动选择的参考而引入额外的错误。本文将选取不锈钢平底洞做为实验试件，以直观的VC软件处理结果来验证这一测厚方法[7]。

　　1理论基础

　　红外脉冲无损检测的原理如图1所示， 可见光(高能闪光灯)对被测试件加热，热流在试件内传导遇到不均匀(有缺陷或有杂质)处热传导受阻，这样缺陷上方试件表面出现热异常，热像仪记录所有热变化的过程并通过数据线传送到计算机。

　　图1 脉冲红外热成像框架图

　　Fig.1 Sketch map of pulsed thermographic

　　在给定特殊热源函数和边界条件的前提下，通过求解热传导方程可以得到表述热波在媒介中传播的函数热扩散方程：

　　热传导方程为：

　　(1)

　　对半无限大均匀介质的热传导方程为：

　　(2)

　　其中：

　　表示单位面积施加在表面的热量

　　为被测试件的蓄热系数，

　　如果材料中有缺陷或者是结构异常，那么一维热传导方程为：

　　(3)

　　根据一维热传导模型，红外热波实验的被测试件热对比度(缺陷中心处和无缺陷处的表面温差)可以表示为：

　　(4)

　　其中：

　　是热扩散系数，代表了材料传导热的能力。

　　是被测试件厚度(或缺陷深度)，

　　为脉冲传播到两种材料界面发生的

　　次放射。

　　热对比度峰值法(PCT法)是直接利用

　　的峰值对应的时刻作为特征时间

　　，特征时间的大小与缺陷深度的平方成正比。热对比度变化率峰值法(PST法)是

　　的一阶导数峰值对应时间作为特征时间

　　，特征时间也与缺陷深度的平方成正比，而与缺陷大小没有关系[1]。

　　对数温度-对数时间曲线分离法(PSDT法)是以对数温度-对数时间的二阶微分峰值时间作为特征时间

　　， 不需要选取参考区域。

　　以对数温度-对数时间的一阶微分为：

　　(5)

　　它的二阶微分为：

　　(6)

　　其中 ：

　　(7)

　　(8)

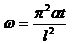
　　(9)

　　当

　　时，

　　取得最大值，此时对应时间即为特征时间

　　，其大小为：

　　(10)

　　从(10)式可以看出被检测试件材料一定时，热扩散系数能确定，缺陷深度的平方与其表面对数温度的二阶微分峰值时间成正比。通过以上理论分析可以知道，参考区域的选择会使结果有不确定性，引入额外的误差，利用二阶微分对数时间曲线的峰值时间不需要选取参考区域，使得特征时间的重复性较好，更适合工程化检测的需求。本文将选取工业中常见的不锈刚材料作为探测对象，用对数温度二阶微分峰值时间作为缺陷深度测量的特征时间[4-5]。

　　2实验试件选取

　　选取尺寸是长300mm，宽200mm，高20mm的不锈钢作为实验试件，底部设计6个深度不同的平底洞，每个平底洞的直径均为20mm，厚度分别为1mm，2mm，3mm，4mm，5mm，6mm，分别记为1，2，3，4，5，6，其背视图和实物图如下图所示。

　　(a)

　　(b)

　　图2 (a)不锈钢平底洞尺寸图

　　(b)试件实物图

　　Fig.2 (a)Sectional drawing of stainless steel flat bottom holes

　　(b)Image of the sample

　　实验所需的红外热波实验装置是图1所示，通过两个4.8kJ的闪光灯给试件的底部施加平行的脉冲热源，选用焦平面制冷型热像仪，图像大小为320×240像素，敏感波段是8um-9um。热像仪广角镜头与试件的距离约40cm，在实验进行过程中是将试件的检测平面正对热像仪，因此缺陷越浅的洞越早得显现出来[6]。

　　3软件计算及结果分析

　　3.1软件计算

　　试件表面的降温过程用热像仪以60Hz的频率采集30s，总共1800帧图像，文件保存为dcb格式。在t=6s时不锈钢试件的二维红外热图如图3所示。图中能清晰地看见6个平底洞缺陷的位置，根据热波传导理论很容易知道出现越早亮度越大的平底洞缺陷越浅，但是不能定量地指出它们的大小关系[8-9]。本文将通过对数时间-对数温度的峰值时间确定出特征时间，求出缺陷深度，并将深度结果以二维视图的方式直观表现出来。

　　图3 t=6s时的红外热图

　　Fig.3 Infrared image at t=6s

　　dcb文件存储的数据格式是：高位数据，高位个数，低位数据，低位个数，经过简单的转换可以直接读取每一帧的各点温度值，进而数据处理和计算。dcb文件数据处理的顺序是：提取文件数据 - 减背景操作- 数据归一化- 数据拟合-PSDT法计算。

　　本实验采取放射式采集，在VC编程处理数据的时候减去背景可以增强对比度，一般选择前十帧温度的平均作为背景。提取6个缺陷区域表面的温度时间信号，为减小误差在缺陷中心选取3×3像素数据的平均值来计算。由于铝的热扩散系数高，采集频率比较高，升温和降温过程都非常迅速，直接拟合会出现较大误差，只关注红外热图的降温过程，并取对数时间-对数温度的降温曲线拟合可减小误差。考虑单点标定测量深度可能产生较大的随机误差，拟合利用最小二乘法多项式拟合，其结果如图4所示。在一维的热传导模型下，热流在缺陷处先放射回来呈现出比无缺陷区高的温度，缺陷越浅升温越快降温也越迅速。 经过归一化的拟合曲线也能看出六个洞的缺陷深度关系。(以下6个平底洞的计算坐标均采用缺陷中心点3×3范围的平均温度计算)

　　图4 六个平底洞归一化并拟合后拟合的曲线

　　Fig.4 Normalization and fitting curves of the six flat bottom holes

　　图5 各缺陷的对数温度-对数时间二阶微分曲线

　　Fig.5 Second-order derivatives of defects lnT-lnt curves

　　由图5可以看出缺陷深度越浅对应的降温过程越迅速，热图上越早出现热异常。缺陷深度不同对应的峰值时间也不同，缺陷越浅，对数温度-对数时间曲线的峰值时间越小。

　　3.2结果分析

　　由于缺陷深度大小的平方与特征成正比，利用这个关系可以通过对数温度峰值的最大帧数确定出特征时间，继而求得缺陷深度。试件的每个缺陷与其对数二阶峰值时刻的关系见表1所示。分析可知缺陷深度较小的计算结果误差比缺陷深度大的误差大，其原因是本文的测厚方法是基于一维热传导模型分析得出，这就假定了半无限均匀的介质的热传播，而实际热传导过程会受三维热扩散和有限尺寸的影响。

　　表1缺陷的对数温度二阶微分对应的特征时间及计算结果

　　Tab.1 The logarithmic temperatures second-order derivative peak time of defects and the compute result

　　缺陷设计(mm)123456

　　峰值对应帧513264180122

　　特征时间(s)0.08370.21670.42840.86171.3342.033

　　计算值(mm)1.1211.8072.5413.6044.4835.536

　　已知不锈钢的热传导系数

　　，利用(10)式计算出以上六点的缺陷深度，图6是选取行号为87和160的缺陷深度曲线，从曲线的分布可以看出6个缺陷深度的大小与试件无缺陷区域的对比。

　　图6 不锈钢缺陷深度曲线

　　Fig.6 Defect depth of stainless steel curves

　　图7 平底洞深度二维图

　　Fig.7 Depth 2D drawing of flat bottom holes

　　图8 平底洞缺陷深度三维图

　　Fig.8 Depth 3D drawing of flat bottom holes

　　以上两图是不锈钢试件所有区域的深度二维图和三维图，可以看出6个平底洞缺陷深浅关系，但缺陷边界有较大的误差，在中心区域深度测量效果理想。二维深度视图比直接用红外热像仪采集的热像图清晰，也实现了定量测量的目的，三维视图的结果具有直观性和量化性。

　　4结论

　　本文选取不锈钢作为试件试件在底部设计6个深度不同的平底洞缺陷，基于脉冲红外热激励的一维传导模型理论，结合对数温度的二阶微分峰值时刻与深度平方成正比的关系，对试件的厚度进行了软件编程自动计算。由理论分析可知PSDT法不需选择参考区域，这就降低了因参考区选择失误带来的误差，通过VC软件编程实现文件数据的提取和计算。数据处理时结合不锈钢热传导快的特点，对采集数据先进行归一化，再采用最小二乘法拟合降温曲线，用对数温度的二阶微分峰值作为特征时间，以此求得个缺陷点的缺陷深度。实验结果表明，用PSDT法软件实现自动测量试件深度，方法具有可行性，计算结果比较准确，获得的深度分布图直接美观，可应用于工业化的自动测量。

　　参考文献

　　[1] Sun J. G.. Analysis of pulsed thermography methods for defect depth prediction [J]. J. Heat Transfer, 2006, 128(4):329

　　[2]Zhi Zeng.Depth prediction of non-air interface defect using pulsed thermography[J]. NDT&E International 48(2012)39-45

　　[3]C.I.Castanedo,X.Maldague.Defect depth retrieval form pulsed phase thermography: Depth retrieval with phase[D].University of Laval Ph.D. Dissertation.2005

　　[4] Zhi Zeng et al.Specified value based defect depth prediction using pulsed thermography[J].Journal of applied physics 112, 023112(2012).

　　[5]Sun J.G. .Method of determining defect depth using thermal imaging[J]. US,6542849[P].2003-4-1

　　[6]HUO Yan, ZHANG Cun-lin.Quantitative infraredprediction method for defect depth in carbon fiber reinforced plastics composite[J](霍燕，张存林.碳纤维复合材料内部缺陷深度的定量红外检测.物理学报)，2012第61期144204.

　　[7]ZENG Zhi,TAO Ning,FENG Li-Chun,ZHANG Cun-Lin.Adopting the ratio of defect size over depth to quantitatively study the effect of defect size on th measurement of defect depth[J]( 曾　智，陶　宁，冯立春，张存林. 采用缺陷宽深比系数定量研究缺陷尺寸对缺陷深度测量的影响. 中国激光),2011.第38卷.

　　[8]ZHANG Xiao-Chuan.Measuring defect diameter and depth in thermal pulse video thermography nondestructive testing[D]( 张小川. 红外热播无损检测技术中缺陷尺寸的测定.首都师范大学硕士学位论文).2006.6

　　[9] Xian Ming-Le ,Xu Zhen-Gao,Yang Xiao-Lin.Automotive measurement for defect depth of composite material in infrared nondestructive testing[J](先明乐,徐振高,杨小林. 红外热波检测复合材料时缺陷深度的自动测量.NDT无损检测 )第31卷第6期(2009).