测量系统的基本定义:
测量:是指对具体事物赋予具体的值的过程。赋予的值不一定是具体的数据,也可以是OK/NOK 或者一等品/二等品/三等品等等的状态。
量具:任何用来获得测量结果的装置。包括通过/不通过装置。
测量系统:是用来对被测特性定量测量或定性评价的仪器或量具、标准、操作、方法、夹具、软件、人员、环境和假设的集合;特别需要说明的是,测量系统不只是检具。
测量系统分析:是指运用统计学的方法对测量系统进行评估,在合适的特性位置测量正确的参数,了解影响测量结果的变异来源及其分布,并确认测量系统是否符合工程需求。
测量系统一般有两种应用范围:
1、用于产品控制:简单的说,就是能否有效区分这个产品是合格还是不合格。
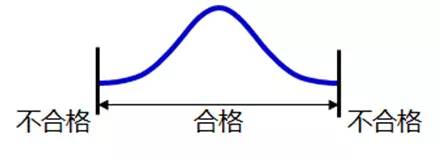
2、用于过程控制:简单的说,就是能否有效的区分制造过程的波动,把过程变异(波动)有效的分为足够多的分组。
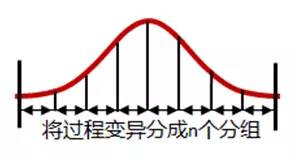
以上两个分类非常重要,在具体的计算方法中,根据这两种分类,可以引出“过程比”和“公差比”的概念。
理想的测量系统是不存在的,无论何种等级的测量系统。总会存在判断错误的风险。如下图所示:
1、不合格区:不合格的零件无论如何测量,总是称为不合格的。
2、风险区:可能会做潜在的错误决定。
3、合格区:合格的零件无论如何测量,总是称为合格的。
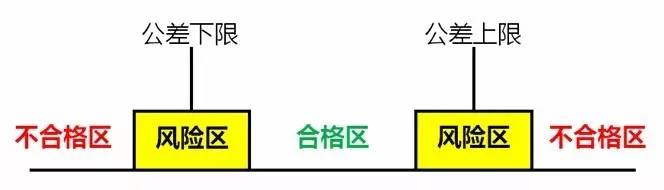
上面的图形表示了这样一个事实:无论采用何种测量系统,只要产品特性落在风险区,总有判断错误的可能性存在(除非风险区的宽度是0,但是这种理想的状态并不存在)。
所以,测量系统分析的本质是判断测量系统的误差是否足够小,能否满足实际的使用要求。
测量系统的误差分为两类:准确性误差和精确性误差。
准确性误差:多次测量结果的平均值和参考值(理论真值)的差异。注意:只要能够获得标准件的参考值,准确性误差就可以获得相当程度的修正(补偿)。因此,在实际的过程控制中,准确性误差的影响并不是很显著。
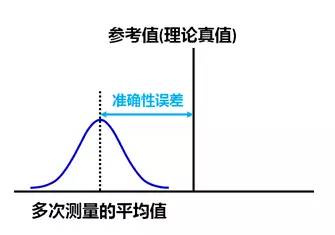
注:参考值(理论真值)可以通过更高一级的测量系统对标准件多次测量取平均值获得。
精确性误差:多次测量结果的每个值和平均值的差异,通常对多次测量数据集合计算标准差,采用6倍标准差来定义精确性误差。
注:通常,精确性误差总是存在的,虽然有一个应对的方法可以适当的减小精确性误差的影响,但是一般不推荐长期使用。
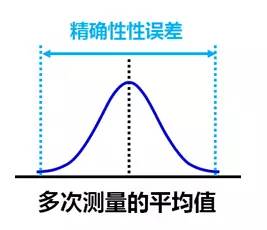
由于测量系统精确性误差的存在,因此实际上,我们用测量系统测量得到的数据,实际包含了两部分的变异(波动):
“制造过程本身的变异(波动)”+“测量系统的变异(波动)”
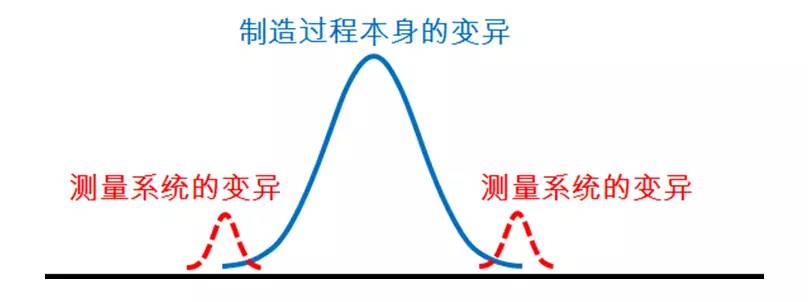
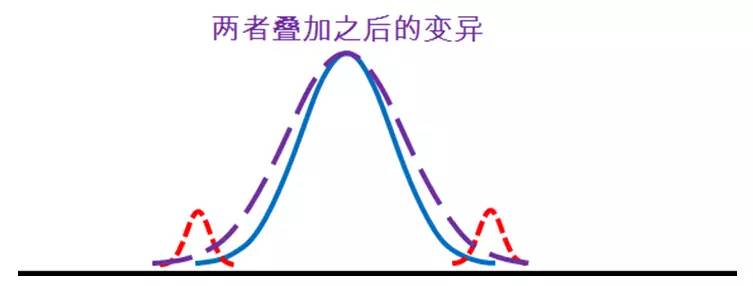
两者叠加后,总的变异变大了。我们用测量系统测量得到的过程数据,都是两者叠加的结果。
下面的方程是测量系统分析的基本模型。
总变异(方差)等于实际的制造过程变异(方差)和测量系统变异(方差)的“简单相加”。
注:上面的表达式揭示了一个现实问题,用测量系统测量实际产品后得到的数据的变异(波动),要比实际的制造过程变异(波动)要大一些,因为里面包含了测量系统的变异(波动)。
将上式两端开根号,可得:
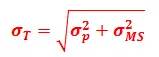
后续我们会用到这个公式。
精确性误差是客观存在的,并且无法用简单的方法加以改善,因此我们关注重点是:测量系统的精确性误差是否足够小。
评价是否“足够小”的指标是用比例。接下来我们引入“过程流”和“公差流”的概念。
1. 过程流的指标,过程比,用6倍的测量系统变异(标准差)除以6倍的总变异(标准差)。

注:分子和分母都有6,可以约分处理。
根据测量系统分析的基本模型,上面的表达式可以进一步分解:
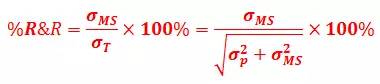
2. 公差流的指标,公差比,用6倍的测量系统变异(标准差)除以公差带宽。
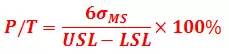
两种流派对于精确性误差的评价指标,要求见下表

注:对于“关键/重要/一般特性”,按照设计的要求来给予分类。
了解了以上问题之后,自然而然的会提出一个疑惑,由于测量系统精确性误差的存在,用测量系统测量得到的数据,实际包含了:“制造过程本身的变异(波动)”+“测量系统的变异(波动)。
那么,在计算过程能力指数C_p时,由于总变异(标准差)包含了测量系统的变异(波动),是否会导致过程能力指数C_p被严重低估呢?

1. 设为实际得到的(包含测量系统变异)过程能力指数,设为理想的(不包含测量系统变异)过程能力指数。设%R&R为过程流的指标。在已知的情况下,给出两者的关系式:
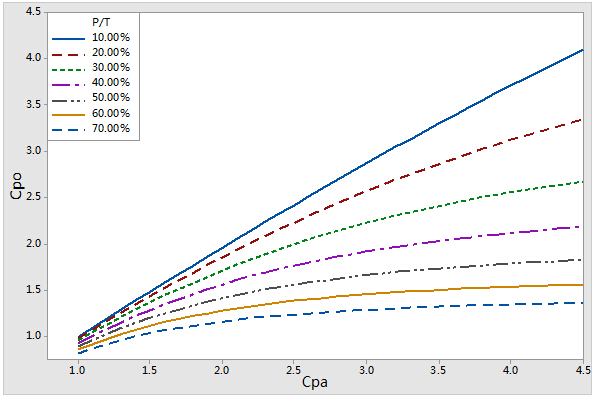
下图给出了不同%R&R情况下,两者的对比关系。
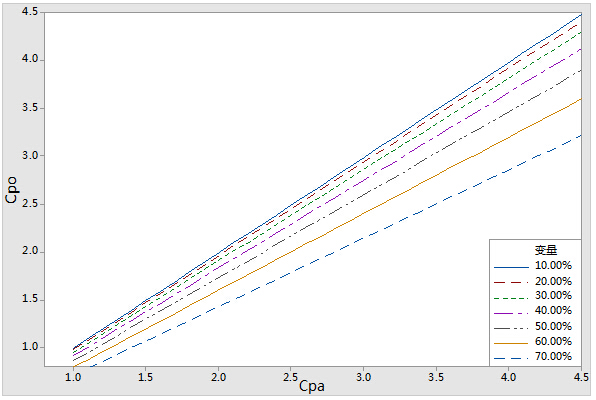
2. 设为实际得到的(包含测量系统变异)过程能力指数,设为理想的(不包含测量系统变异)过程能力指数。设为公差流的指标。在已知P/T的情况下,给出两者的关系式:
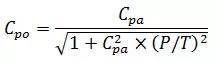
下图给出了不同情况下,两者的对比关系。
下面的表格,详细的列举了一些数据的计算结果,从表格里可以发现,和之间存在差异,但是这个差异非常小。
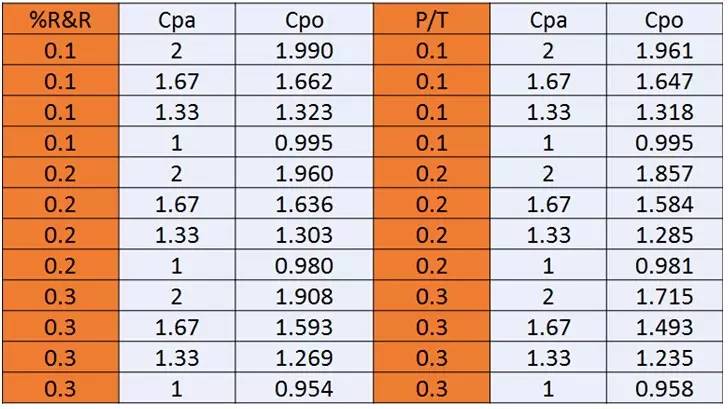
对于测量系统变异对过程能力的影响的疑惑,结论是:影响是存在的,然而在给定的要求内,这个影响非常小,可以忽略。(来源:网络)